Love Oscillations I

Review

Debanuj Chatterjee

  

Tweet

  Margherita got into the cab in tears. It was her fifth breakup with Raphaël, her classmate in the University. It was raining outside. As the cab gushed through the shimmering streets, her eyes were transfixed on the oscillating motion of the wipers of the car. She was living the lives of those raindrops that flew through the clouds all the way down to hit a car screen and eventually be scathed away by petty wipers. Before she lost herself into deeper bubbles, she gathered herself and said, “I am not going to patch up with him again”. But promptly she realized she had said the same thing after her last five break ups with him. “Am I trapped in an endless loop?” she asked herself. “Calm down Margherita, çava, çava..” she tried to tone down her barometer. “I will figure out why I am in this loop, and I will get out of it”, she pledged to herself. The rain had suddenly stopped, and the wipers were off; she brought down the car’s windowpane, looked outside, and ignited her analytical thought engine.

  Margherita studies Physics in the old Sorbonne University of Paris. She trains in how to use the language of mathematics to describe the zoology of phenomena that we see around us in the real world. Love is another such physical phenomenon, however a very complicated one to deal with, since it involves human interactions. “So, is it possible to gauge the modus operandi of the dynamical evolution of my relationship with Raphaël? Or at least the shadows of the complicated mechanisms that drive our romantic cycles?” Margherita thought on her way home. Reaching home she started preparing for her quest with her old friend, Google. While surfing through the waves of information, Google sniffed her situation and a famous song on the nature of love by George Gershwin popped up in a corner from nowhere. The beautiful song caught her attention and she started listening to it :

“When you want em, you can’t get ‘em,
When you’ve got ‘em, you don’t want ‘em…”

Margherita heard this song numerous times when she was in middle school, but had never dug into the heart of the lyrics. But today the sweet melody could not saturate her enthusiasm, and suddenly the lyrics made sense to her like broad daylight. She pictured Raphaël’s love for her in the song. When she is angry at him and ignores him, he suddenly shows a lot of love and care and woos her with attention, while when she starts loving him back, his enthusiasm for her slowly dips and he becomes less responsive with time. With a hazy frown, Margherita picked up her notebook and a pencil. She started scribbling: Let us suppose, we denote M(t) [M varies with time, denoted as t] as the love of Margherita for Raphaël and R(t) as the love of Raphaël for Margherita. Now both M(t) and R(t) change with time. But what is the rule by which they are changing? If we denote dR/dt as the rate of change of R¹, with time (i.e. how much R changes in a very small interval of time, i.e. dt), then probably dR/dt/=-aM, where a is some positive number. This clearly means, when M is positive (i.e. Margherita loves Raphaël), Raphaël’s love for Margherita decreases. On the other hand, if M is negative (i.e. Margherita starts ignoring him), Raphaël’s love for her increases.
¹To simplify the notation we write R(t) and M(t) as R and M respectively.

  Margherita was quite intrigued by her observation. She kept moving forward with her analysis. She further wrote down, dM/dt=bR, where b is a positive number. Consequently this meant Margherita's love for Raphaël increases as Raphaël loves her back. So now she has two differential equations describing the rate of change of R and M with time. The next step is to find the mathematical solution to R and M, i.e. how exactly R and M evolve with time.

  Differential equations are ubiquitous in physics. Being a student of physics, it was easy for her to find a solution to these equations. Considering the simple case of a=b=1, the solution to R and M looked like this :

R(t)=cos(t), M(t)=sin(t)/,

where at time t=0, she considered R(0)=1 and M(0)=0, since it was Raphaël who fell in love with her at first sight, while her love for him developed gradually. To visualize it she plotted R and M in Fig. 1. :

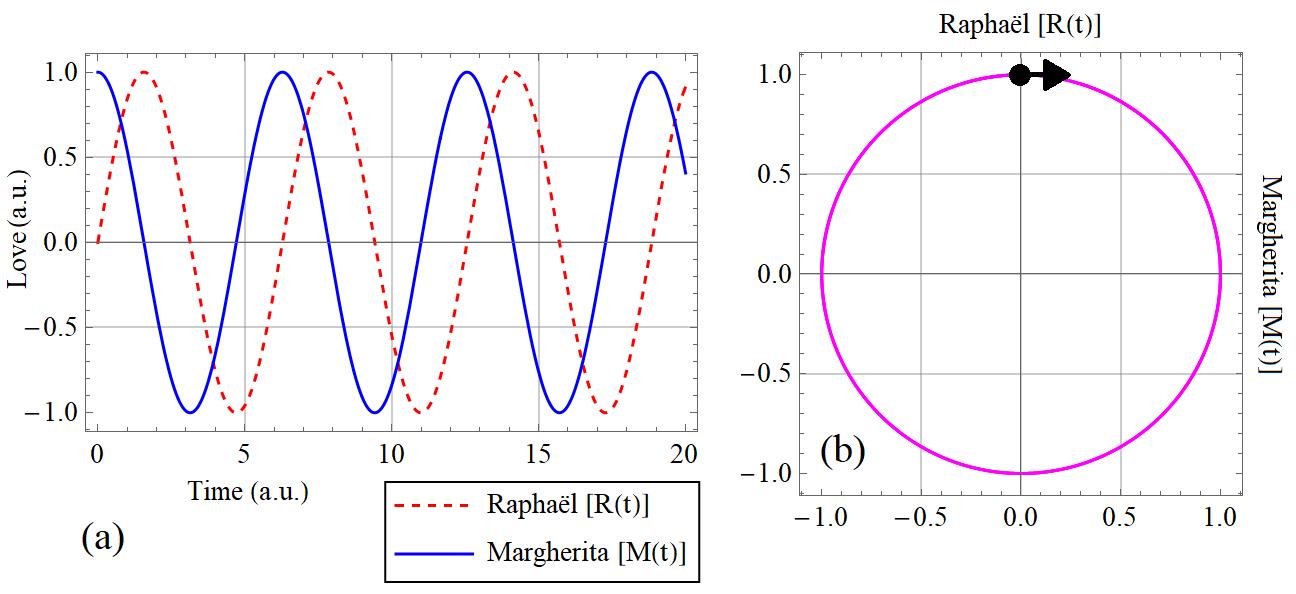Fig. 1. (a) Evolution of the love of Raphaël [R(t)] (red dashed) and Margherita [M(t)] (blue solid) as a function of time. (b) Phase space diagram of R(t) and M(t). a.u. : arbitrary units.   From Fig.1(a), it is clear that both R and M oscillate with time; however, the curves are not in sync, as they are shifted in the horizontal direction with respect to each other. Similarly, Fig.1(b) shows how the system evolves in the R-M plane. The black point, which represents the system at a particular instant of time, moves along the magenta trajectory, as shown with the black arrow.

  The entire picture became clear to Margherita. However, her goal was to avoid falling into such oscillatory loops. She thought for a while and asked herself, “What if I have dR/dt=aM, instead of dR/dt=-aM?”². She figured out in that case, the solution for R and M would be :

R(t)=cosh(t), M(t)=sinh(t),

where cosh and sinh are cosine hyperbolic and sine hyperbolic functions respectively. Unlike sine and cosine that oscillate with time, sinh and cosh functions grow exponentially with time [see Fig.2(a)]. That means with time their love will grow indefinitely. Although indefinite growth is not a physical possibility, the notion here is that their romantic relationship would not oscillate in cycles of love and hate, rather grow towards a stabilization.
²Note that here we consider a to be a positive number.

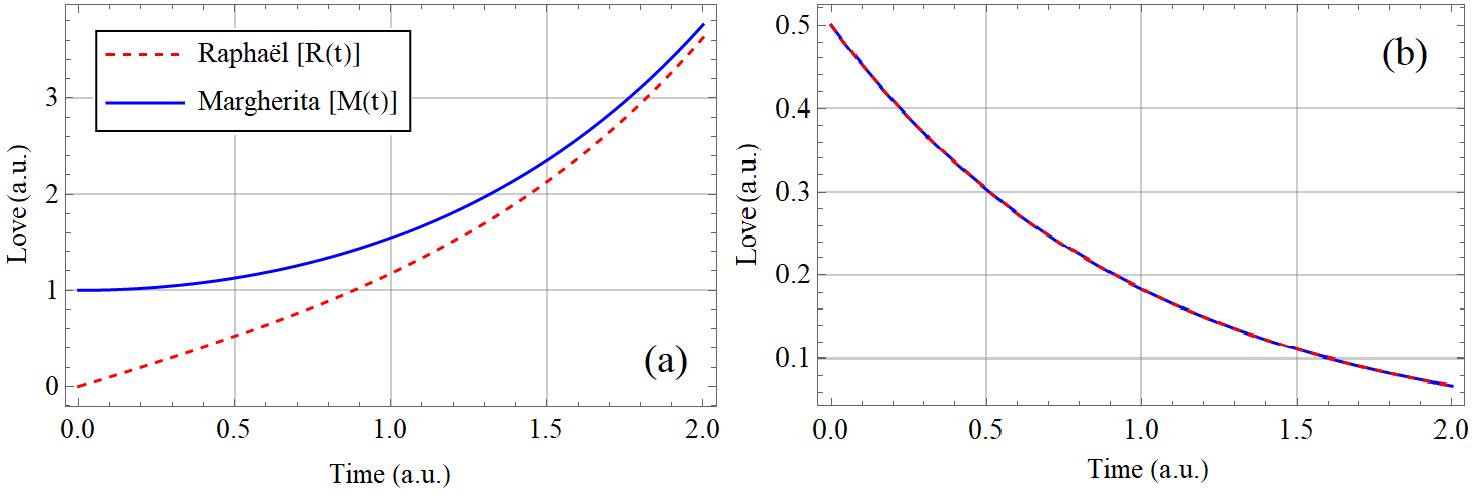Fig 2. (a) Time evolution of love of Raphaël [R(t)] (red dashed) and Margherita [M(t)] (blue solid), as obtained from solving dR/dt=aM and dM/dt=bR, with R(0)=1 and M(0)=0. (b)Same as (a), except solving dR/dt=-aM and dM/dt=-bR, with R(0)=0.5 and M(0)=0.5. A.u. : arbitrary units.   In a similar way, she thought, if the equations were dR/dt=-aM and dM/dt=-bR, the solution would be :

R(t)=Exp(-t)/2, M(t)=Exp(-t)/2,

where Exp refers to the exponential function. To obtain this solution, R(0)=M(0)=0.5 was considered. The solution implies that their love for each other would continually and exponentially decrease with time, indicating a permanent mutual apathy [see Fig. 2(b)]. Therefore, if the right hand side of each of the equations have the same sign, then their relationship would not acquire the oscillatory characteristic that she is bothered about; it would either stabilize into a permanent happy relation, or lead to a state of perpetual apathy (for at least one of them). Content with her analysis, she went to sleep that night with a hope of stability in her life. But a pinch of anxiety kept leaking in her headspace. Her state of mind approximately reverberated with Alicia Keys’ words :

“I keep fallin’ in and out of love with you. Sometimes I love ya, sometimes you
make me blue. Sometimes I feel good, at times I feel used. Loving you darlin’ makes me so
confused.”.

  The next day Margherita’s inbox was overflowing with messages from Raphaël. He was sorry for the breakup, and the same old drama was about to repeat again. Margherita quietly read his messages and did not reply to him. In the evening, she penned down her thoughts and emailed them to Raphaël. She was evident in her views, summarised as: “We are in a precarious cycle which cannot go on forever. I show you the simple model that explains our repeating emotional cycles. Please figure out a solution to change your fickle love, and hence the equations of our relationship. Preferably a permanent breakup plan should be chalked out so that we can breathe in peace.”. She waited anxiously for Raphaël’s reply. But it did not come until two days later. The response was not something she was expecting. Raphaël never failed to surprise her.

  Raphaël is also a student of physics, like Margherita, however, he is more methodical with a fancy for perfection. His reception of Margherita’s email was calm and soft. Instead of agreeing to Margherita’s model, he started digging into the problem deeper. What he replied to her can be summarised as :

“I am elated to find your indulgence in this important life problem. Appreciating all your efforts, I must say, your pursuit made you embark on the Strogatzian model of love affairs[1]. However, Tennyson says, “In the spring, a young man’s fancy lightly turns to thoughts of love.”. In this context, this means that the style of a lover’s love, characterised by a and b, can actually be time-dependent rather than constants. Even if we agree to keep a and b as constants, I would suggest a more general model for this purpose, which can be described as :

dR/dt=pM+qR,
dM/dt=rM+sR,

where p, q, r and s are positive or negative constant real numbers that characterise our romantic styles. The idea here is that the rate of change of anyone’s (either Raphaël or Margherita) love is not only dependent on the partner's love for him/her, but also depends on his own love for the partner. Note that, with q=r=0, p<0, s>0, we retrieve back your model of the romantic pendulum, i.e. Strogatzian love. q=r=0, p>0, s>0 and q=r=0, p<0, s<0 lead to indefinite love or indefinite hate situations respectively, as you also propose [see Fig. 2(a)]. However, there can be other possible situations, for example, p>0, q<0. In this case, since q<0, I (Raphaël) am discouraged by my feelings towards you. However, since p>0, I respond positively to your (Margherita’s) affection towards me. To clarify the subtlety of the meaning of q<0, I reiterate that when R is positive since q is negative, qR is negative, and hence R decreases, i.e., R self-suppresses itself and prevents its steep growth. Such is the trait of a cautious lover. Similarly, p<0 and q>0 are close traits of a narcissistic nerd! q and r can be considered parameters that quantify behavioural inertia, whereas p and s are the parameters quantifying the strength of the partner’s influence[2]³.
³Take a pause and think about it for a moment if you are confused.

  Interestingly, according to this model, the way to get out of the love-hate oscillating loop is not that difficult. Before understanding the strategy, let us first make some simplifying approximations. We assert here that q and r are much smaller than p and s. This means that the change in the lovers’ love is primarily influenced by the love of the partner and minimally affected by his/her own love towards the partner. Considering this assumption, and also the fact that p is negative and s is positive (from Margherita’s model), it can be shown that the qualitative behaviour of the system depends only on the quantity q+r (Can you figure out why? See Ref. [3], Chapter 4 therein). Now, q+r=0 leads to the traditional oscillatory behaviour, where the system moves on a circle (or more generally an ellipse) in the phase space, as shown in Fig.1(b). However, when q+r>0, the the system spirals out into infinity [see Fig. 3(a,b)] implying an increase in mutual love, whereas for q+r<0, the system spirals in to the origin [see Fig. 3(c,d)], leading to a state of mutual apathy, and hence an end to the relationship.

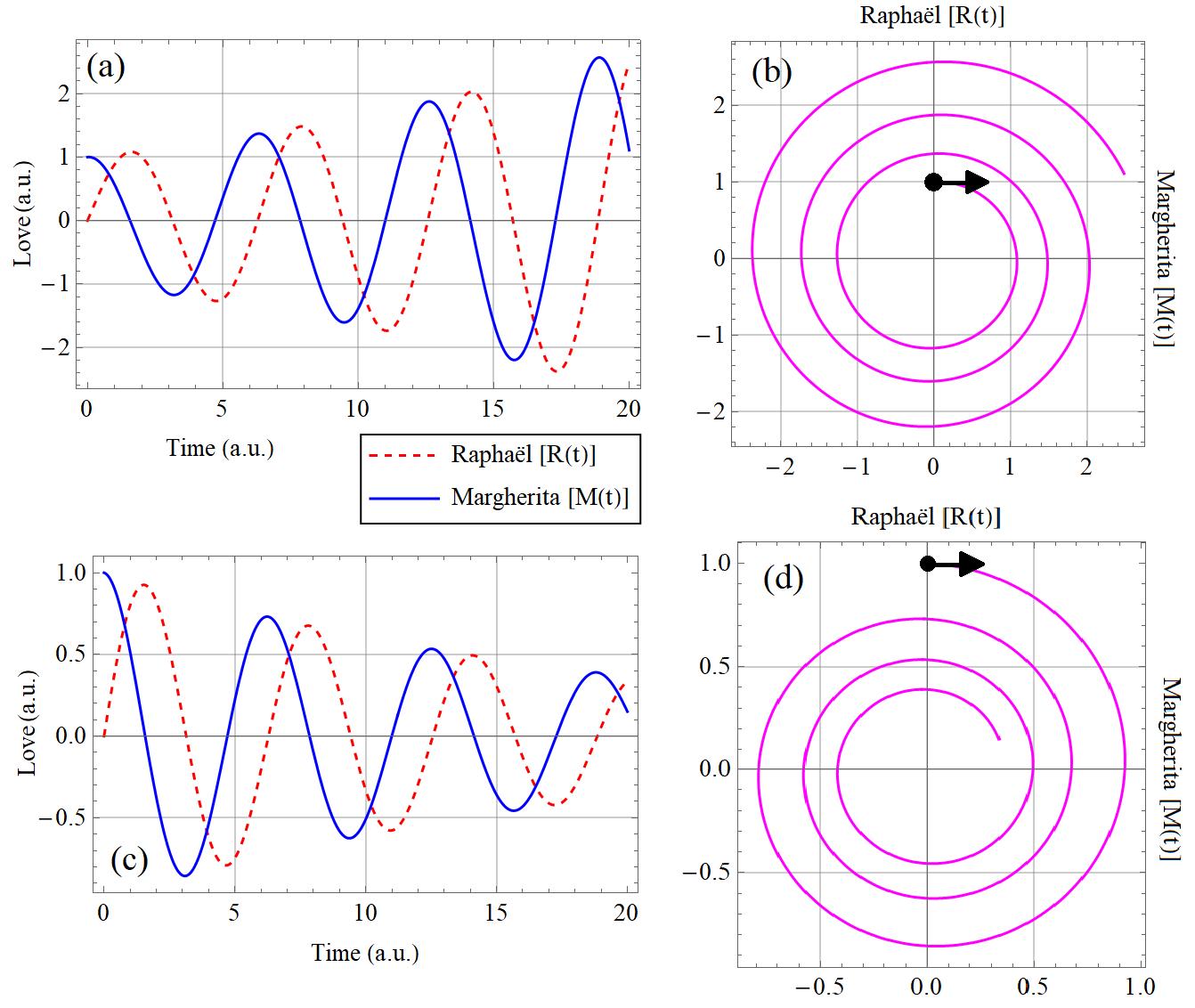Fig. 3. (a,c) Plot of time evolution of love of Raphaël [R(t)] (red dashed) and Margherita [M(t)] (blue solid), as obtained from solving dR/dt=pM+qR and dM/dt=rM+sR, with R(0)=1 and M(0)=0, when q+r>0 [for (a)] and q+r<0 [for (c)]. (b,d) Corresponding phase space diagram of R(t) and M(t) when q+r>0 [for (b)] and q+r<0 [for (d)]. a.u. : arbitrary units.   Therefore, to break out of the loop, both of us need to do either of the following. 1. Tilt our romantic styles a bit towards narcissistic love, i.e. we let our loves be positively influenced by our own love towards each other. In such a case, q>0 and r>0 implying q+r>0. It will lead to an eventual increase in love, as indicated in Figs.3.(a,b). 2. Self-suppress the love towards each other, i.e. negatively influence our loves towards each other, similar to a cautious lover. In that case, q<0 and r<0, and hence q+r<0. With time, this will lead to a mutual decrease in our love, and we will break out of the loop, as shown in Figs.3.(c,d).

  Nevertheless, these linear models might often reside very far from reality, simply because human interactions involve a large number of independent parameters that are not accounted for in the model. Such parameters can arise from a variety of sources, such as the influence of other individuals on someone’s relation, effects of mood swings, effects of communication gap between the partners, other kinds of distress in daily life, etc. However, a more advanced model can be found in the literature, trying to incorporate the effect of these other factors as random fluctuations in the system. Such modelling indeed reveals a more complicated dynamic of emotional interaction between couples[4]. These models can also be related to the cycles of happiness in a man’s life[5].”

  Margherita was happily disappointed with Raphaël’s reply. His reply was a bit too technical and insipid to her, lacking the touch of emotion that she was expecting. On the other hand, she felt a taste of narcissism in the response, which according to his theory is supposed to be a good sign after all. She sighed as her mind resorted to the tune of Gershwin, “A little loving now and then, is relished by the best of men".

  Gazing at the sunset from the window, she stumbled upon another striking idea: What if their emotional evolution is also influenced by a third party that she does not know about? Is there another woman who also influences the behaviour of Raphaël towards her? A triangular system? Can it be Maria, his childhood friend? Margherita gasped as she was getting lost in the maze. However, the soothing orange of the evening sky averted her mood from such scepticism. She shooed away the thought for the time being and planted the idea in her head for a future sprout. For now, she started getting ready for another lap of the romantic cycle with Raphaël.

  The dusk dawned with new stars, and she named her little pet cactus Raphaël. Thorny, but clever and green. (to be continued...)

  P.S.: About two-thirds of young dating adults have experience with on-and-off relationships that often seats them in an emotional rollercoaster wreaking havoc on their mental well-being[6]. Psychological analyses of such relationships are well studied in the literature[7], and most of them point towards a predominantly negative impact on the social health of the associated parties[8]. This series aims at understanding the origin of such love oscillations through the mathematical lens in a fictional setting.

  P.P.S.: Margherita Luti, or more famously known as La Fornarina (baker’s daughter), is suspected to be the secret lover of the celebrated Renaissance painter Raphael. The unfolding of their romance was secretive and mysterious. As the story goes, Margherita, despite her love for him, did not agree to marry Raphael.^4
4The exact identity of La Fornarina, and the associated sequence of events is still highly debated.

Bibliography

1. Strogatz, Steven H. "Love affairs and differential equations." Mathematics Magazine 61, no. 1 (1988): 35-35.
2. Sprott, J. C. "Dynamical models of love." Nonlinear dynamics, psychology, and life sciences 8, no. 3 (2004): 303-314.
3. Kreyszig, Erwin. "Advanced Engineering Mathematics 10th Edition." (2009).
4. Wauer, J., D. Schwarzer, G. Q. Cai, and Y. K. Lin. "Dynamical models of love with time-varying fluctuations." Applied Mathematics and Computation 188, no. 2 (2007): 1535-1548.
5. Sprott, J. C. "Dynamical models of happiness." Nonlinear Dynamics, Psychology, and Life Sciences 9, no. 1 (2005): 23-36.
6. Dailey, René M., Abigail Pfiester, Borae Jin, Gary Beck, and Gretchen Clark. "On‐again/off‐again dating relationships: How are they different from other dating relationships?." Personal Relationships 16, no. 1 (2009): 23-47.
7. Dailey, René M., Borae Jin, Abigail Pfiester, and Gary Beck. "On-again/off-again dating relationships: What keeps partners coming back?." The Journal of social psychology 151, no. 4 (2011): 417-440.
8. Monk, J. Kale, Brian G. Ogolsky, and Ramona F. Oswald. "Coming out and getting back in: Relationship cycling and distress in same‐and different‐sex relationships." Family Relations 67, no. 4 (2018): 523-538.