Fractals: A New Way of Understanding Visual Arts

Review

Debanuj Chatterjee

  

Tweet

  What is beautiful and what is not? How to define or identify beauty? Man has asked and tried to answer these questions through the ages. Nevertheless, despite being captivating and transcendental, the nature of beauty turned out to be highly elusive. Some say beauty lies in the eyes of the beholder, while others believe in the existence of certain universal rules that can, at least to some extent, characterise beauty. Yes, we can all agree that beauty in itself encapsulates a subjective element that evokes an individual-specific emotive response from the perceiver; but to what extent? Are there algorithms that can loosely classify some things as beautiful and others as not? For example, can an image generated from random noise [see Fig. 1(a)] be beautiful according to a large consensus of individuals? Or can a countryside landscape with vast stretches of greenery coalescing into the horizon [see Fig. 1(b)], be perceived ugly by many? Statistically speaking, the answers to the two previous questions should intuitively be a “no”. Don’t you think?^1
1 Here we are only talking about the aesthetic or face value of the image, rather than its inner meaning.


Fig. 1. (a) Image of random noise (b) A countryside scenery.
(Courtesy: https://freerangestock.com)
  On a fundamental level, both Figs 1. (a) and (b) are made up of a collection of pixels, each pixel having specific intensities of red, blue, and green colours. However, the distribution of those intensities makes one picture look more beautiful than the other. So what is different in the two pixel distributions? If you look carefully, you will notice that although for the noise image, there seems to be no specific pattern in the distribution of black and white pixels, i.e. it is entirely unpredictable, however for the image of the countryside, there are certain patterns. For example, there are patches in the image, where the colour is almost constant (for example parts of the sky, where it is blue) i.e., the spatial colour contrast is quite low, but there are parts where the spatial colour contrast varies very fast (for example on the edges of the clouds). Furthermore, for the second image, we can predict certain features, for example, the green cannot be present in the sky, or the brown path gives us a sense of depth, and hence we understand that the little black patches on the horizon are trees, although we cannot see them in detail.

  Therefore, naïvely speaking, while the complexity associated with Fig 1(a) is quite large (as its pixel distribution is entirely unpredictable), the complexity of Fig. 1(b) is lower than that. However, we should note that the complexity of Fig. 1(b) is not entirely null, too. For instance, the clouds in the sky are still quite randomly distributed. An example of a null complexity image is a completely white (or black) image that contains no information. Thus, from this discussion, we can hypothesize that there seems to be a connection between the human preference of an image, and its complexity. A random noise with large complexity or a white image with no complexity seems to have a lower aesthetic value when compared to one with an intermediate complexity. In fact, this was the core idea of the hypothesis proposed by Daniel Berlyne in 1971, in his book Aesthetics and Psychobiology [1]. Needless to say, it led to an upheaval of debates within the scientific community, which continues to this day.

  So far in our discussion, we comprehended the probable connection between the complexity of a pattern (or image) and its aesthetic value. However, we missed an important point: how do we quantify complexity? Quantification of the complexity of a pattern can be performed in several different ways, one of which is the technique of computing the fractal dimension of the pattern. A short primer on understanding fractals and computation of the associated fractal dimension is discussed below.

  Fractal dimension of an image:

  Fractals refer to a specific class of patterns² that exhibit certain properties, such as self-similarity at different scales of magnification. This means, when we zoom into a fractal pattern, certain properties tend to recur as we keep zooming in. This feature can be explained with the example of the branches of a tree.
²Mathematically speaking, a set of points.

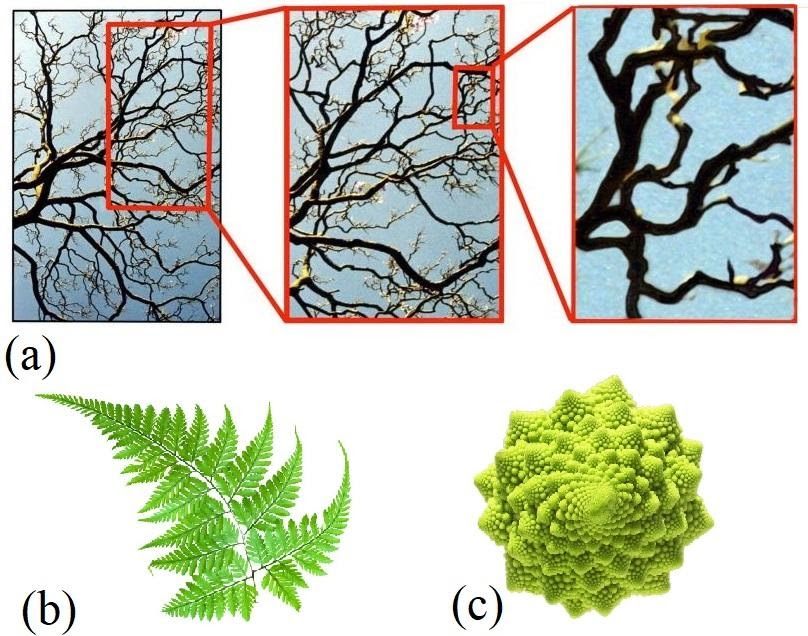Fig. 2. (a) Image of branches of a tree at different magnification levels (increases from left to right). (b,c) A fern leaf and broccoli, which show self-similarity. (courtesy Ref.[3])
  In Fig 2(a), we see the whole image of a tree with its branches on the left. As we move to the image in the middle, which is a magnified version of the image on the left, we see that the magnified image looks more or less similar to the original one. On further magnification, we get the image on the right which also follows the same property. This self-similar property is a signature of a fractal. Although we are limited by just three levels of magnification in this case, a mathematical fractal would allow this self-similar recurrence through infinite magnifying iterations. Some other examples of naturally occurring fractal patterns are leaves of a fern plant [Fig. 2(b)] or the patterns on a broccoli [Fig. 2 (c)].

  From the previous discussion, we understood that fractal structures can be enormously complicated, as they have nested structures (structure within a structure within a structure and so on). Thus naturally they provide a good framework for quantifying visual complexity. In this context, the complexity of a fractal can be defined to be its fractal dimension. What is the fractal dimension? The fractal dimension of a fractal pattern (two dimensional in our case), is a number between 1 and 2, that can be thought of as a measure of the roughness of the fractal. In fact, for any given image (even if the image is not a perfect fractal), its fractal dimension can be computed pretending as if it were a fractal. In that way, we get a crude quantification of the complexity associated with the image. A short discussion on the method of determining the fractal dimension of an image is provided in the Appendix.

  Fractal expressionism:

  Having discussed the complexity of an image, its quantification, and all that jazz, let us now delve a bit into the world of arts. We start from the barn of a small wooden house, in the Springs area of East Hampton in the USA, in March 1952. It was a stormy night. A drunk artist unrolled a large (about 18 feet) canvas across the barn and started dripping paint across it in random directions using a wooden stick. Often in his frenzy, he would throw the paint cans on the canvas with all his might, often he would swirl the paint from a distance in turbulent trajectories. Was this deceptively simple and primitive painting style the manifestation of raw genius? Or was it a drunken mockery of prevalent artistic traditions? As the drippings continued, some kind of abstract yet organic structure started shaping up on the canvas. A few finishing touches were laid at the heart of the night, and the artist signed it as “11, 1952”. Today, this painting is known as Blue Poles: Number 11 (see Fig. 3), which is considered one of the most valuable paintings on the planet! It is currently estimated to be worth a staggering $200 million.

Fig. 3. Blue Poles, Number 11, an artwork by Jackson Pollock. (courtesy: Pollock-Krasner Foundation)
  The artist we talked about is none other than Jackson Pollock, one of the greatest artists of modern times and the leading exponent of the abstract expressionist art movement in post World War II America. His kinetic style and intimate involvement with the process of painting added organic expressions to his artworks. The dripping style of painting that he perfected pushed art to the extremes of abstraction, devoid of perspective, space or narrative. His artworks shifted the emphasis from artificial order towards chaos, energy, spontaneity, nature and a subconscious connection. Subsequently, a diverse group of painters including Jackson Pollock, Mark Rothko, Barnett Newman, etc. in the New York art school, who were curating these bold avant-garde styles of exploring the inner space through their canvases, came to be known as the abstract expressionists.

Jackson Pollock painting (credits- Hans Namuth)
  Interestingly, there were many controversies about the worth of abstract expressionist paintings. Some critics opined positively, stating that these compositions were able to engage the viewer in intimate dialogue, while others often regarded them as a trashy splash of colours on a canvas, no better than a five-year-old would have done. In particular, the Blue Poles, Number 11, by Pollock caught the media attention in 1973, when the Australian government led by Prime Minister Gough Whitlam decided to buy it for $2 million. This led to a huge backlash from a part of the Australian public who considered the deal a waste of taxpayers’ capital. It led to a split in Australian society. People who objected to abstract art and its values were tainted to be traditionalists, and those who championed it became the progressives.

  Richard Taylor, a physicist at the University of Oregon, Eugene, USA, was in seatch of Pollock paintings’ secrets, particularly Blue Poles, Number 11. While investigating the spatial patterns of the artwork in the light of scientific objectivity, to his surprise, he discovered that the painting was a fractal, i.e. it had a self-similar characteristic (just like nature’s fractals). Subsequently, he also found out that most of Pollock’s other drip paintings were fractals too (see Fig. 4 for a comparison with nature’s fractals). Furthermore, it was found that through Pollock’s career, the fractal dimension of his paintings increased with time. It grew from a value near 1 in 1943 to about 1.72 in 1952. Taylor explains this increment as follows: With time, Pollock’s dripping style matured, and thus, his paintings were acquiring more and more complexity and hence an increase in the fractal dimension. Taylor described such artistic expression of Pollock in the form of fractal patterns as fractal expressionism.

Fig. 4. Comparison of natural fractal patterns with one of Pollock’s paintings. (a) Snow on a rock, (b) top view of a forest, (c) part of a Jackson Pollock’s painting, One, Number 31, 1950. (courtesy Ref. [4])
  Human beings show a consistent aesthetic preference towards fractal patterns [5]. Studies suggest that most naturally occurring fractals (e.g., a tree) have a fractal dimension clustered around a value of 1.3. Moreover, psychological studies reveal that images with a fractal dimension in the range 1.3-1.5 seem aesthetically most pleasing to the human eye³. The reason is probably due to overexposure of the human eye to nature’s fractals, which tuned our perceptual space to prefer certain levels of complexity [6,7]. In the case of Pollock, the fractal dimensions of his paintings were mostly in a higher range (~1.7) rather than the proposed sweet range of 1.3-1.5. Nevertheless, the appeal of Pollock’s fractal expressionism might stem from the enhanced complexity of the image that emanates an extra action rather than bliss, to produce a captivating viewer experience [3]. Another possible resolution of this discrepancy might come from the overestimation of the fractal dimension of Pollock’s paintings due to the choice of a different colour filtering method than that is employed by the human eye, while computing the fractal dimension [8].
³There are debates about the exact range of values.

  Visionary art:

  Apart from fractal-like abstract expressionist art, another art form that can benefit from the technique of fractal analysis is visionary art, i.e. art forms that are inspired by hallucinatory visions. In the 1960s, Dr Oscar Janiger, an experimental psychiatrist at the University of California Irvine, was one of the pioneers in investigating the effects of hallucinogenic compounds (like LSD or lysergic acid diethylamide) on human perception. One of his experiments was particularly intriguing. In this experiment, he investigated the effect of hallucinogenic agents on the aesthetic performance of an artist’s brain. To this aim, he gathered some volunteer artists from the locality and exhibited them a little Kachina doll⁴ from his desk. The artists were supposed to draw it on a piece of paper. After that, the artists were infused with a mild dosage of LSD. Thereafter, when the artists’ brains were under the siege of hallucination, they were again asked to draw the same Kachina doll on another sheet of paper. After the session, the before and after LSD drawings were compared. The results were indeed striking (some are shown in Fig. 5)!
⁴Kachina dolls are small dolls resembling a spiritual being called Kachina, from the Pueblo Native American culture. These dolls are given to those who can respectfully take care of the well-being of the doll.

Fig. 5. Pictorial reproduction of a Kachina doll (left) by two anonymous artists before (middle column) and after (right column) registration of LSD in Janiger’s experiment. (courtesy Ref. [9])
  The post-LSD pictures of the artists in Fig. 5 remind us of abstract expressionism; don’t they? In fact, Janiger in his analyses noted the tendency of movement towards a non-representational expressionist style by many of the artists under the drug [10]. In other similar studies by Hoffer and Osmond, they report blurring and distortion of vision of their test subjects under LSD. Their subjects often described their visual experience as a space full of patterns and objects (like lacework pattern, ribbons, little circles, fog or smoke, etc.), disproportionate changes in shapes, intensification of colour, etc. [11].

  The reported changes in the visual perception under psycho-action, as discussed above, ipso facto points us to the question: does the hallucinogen increase the complexity of our perceptual space? In other words, under the influence of these drugs, does the complexity of what we see around us increase? To find an answer to that question, one needs to have a sequence of images representing the visual perception of an individual as they move from a non-hallucinatory to a hallucinatory state of mind. After that, computing the fractal dimension of those images would give us an idea about how the perceptual complexity evolves through the emergence of hallucination.

  On 27th August 2015, a news article appeared in the online newspaper, The Independent, about an artist taking LSD and drawing her self-portraits over different stages of her ten-hour psychedelic trip. The anonymous artist apparently took 200 μg of LSD and drew a sequence of eleven self-portraits (spending between 11 to 45 minutes on each self-portrait), aiming to yield a sort of visual map of her headspace (see Fig. 6) under the influence of the drug.

Fig. 6. Self-portraits of an artist during an LSD trip. The respective times after which the drawings were made, calculated from the time of the drug ingestion, are indicated in hours. (courtesy The Independent)
  A close inspection of the self-portraits indeed reveals a movement towards space-fillingness, inclination towards curvilinear or chequerish motifs through the hallucination journey. To quantify the intuitive observations, the fractal dimension of the images were computed using the box-counting technique (see Appendix). A plot of the fractal dimension versus the time at which it was painted is shown in Fig. 7. In Fig. 7, we see an increase in the fractal dimension from 1.64 to 1.87 for the first two hours. For the next seven hours, it remained more or less constant at an average value of 1.86. At the 10th hour, when the effect of LSD was disappearing, it again decreased to 1.77.

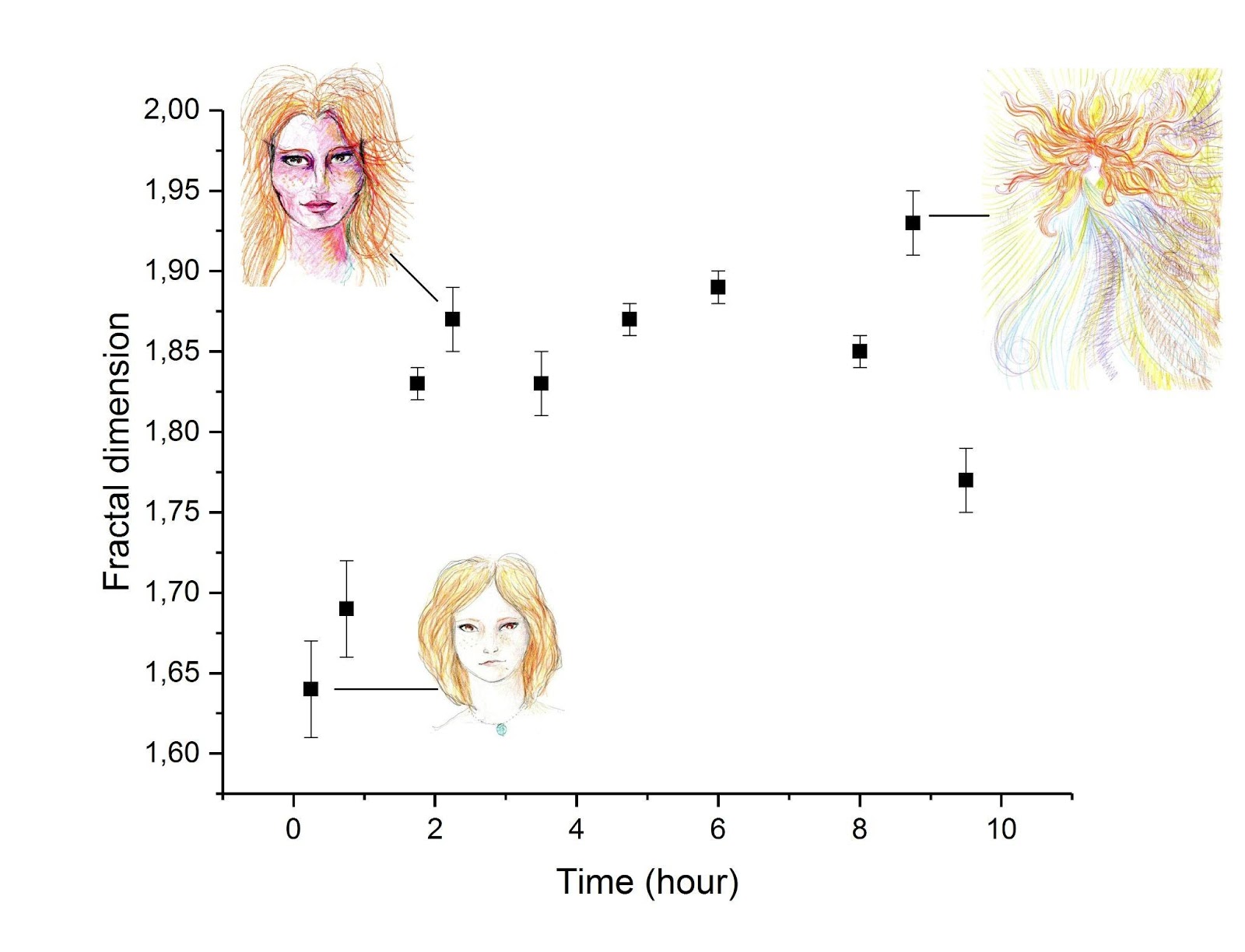Fig. 7. A plot of the fractal dimension of an image (with error bars) vs the time at which it was completed.
  The above analysis might suggest that an artist under the effect of LSD prefers a greater level of detail in an artwork (as characterised by its fractal dimension). This effect is probably caused by an increase in the fractal dimension of the artist’s visual perception, which is in line with the experimental observations of Hoffer, Osmond and Janiger. In fact, research from the group of Dr Anil Seth in the University of Sussex shows that the complexity of our brain, or in other words, how complexly different parts of our brain are talking to each other at a certain moment, increases under the effect of psychedelics like ketamine, psilocybin and LSD. In particular, in their studies, they computed the ⁵Lempel-Ziv complexity, of brain signals under hallucinogenic effects [12]. In another study, the evolution of fractal dimension of an artist’s paintings as she/he undergoes neurological disorders was evaluated by Forsythe et al. and a correlation between the two was hypothesized [13]. All this knowledge makes us wonder if the complexity of an artist’s painting is correlated to their brain’s neural complexity. Hence arises the conjecture : a brain with enhanced complexity leads to the generation of artworks with a higher fractal dimension.
⁵Lempel-Ziv complexity is a widely used complexity measure in neuroscience often employed to evaluate how different parts of the brain are correlated with one another.

  Discussion and Conclusion:

  To conclude, in this article, we talked about the technique of fractal analysis to determine the associated complexity of an image, to gauge its aesthetic value. On the one hand, it helped us understand the appeal of abstract expressionist paintings of Jackson Pollock. On the other, it provided us with some direction in understanding the connection between our state of consciousness and the artwork we produce. Nevertheless, these ideas probably illuminate only the tip of an iceberg remaining to be discovered, and indeed these topics are an active area of research today.

  As one can understand, evaluating the complexity of a given image is a tricky business. There are multiple formalisms to achieve it [14]. In this article, we only talked about the complexity of artworks evaluated through fractal dimension computation. However, there are other paradigms; for example, Gif or Jpeg compression algorithms are often employed for complexity evaluation (which are also used in compressing digital images) [15].

  In terms of future perspectives, the fractal analysis of artworks provides us with a framework for understanding paintings of a large class, such as Jackson Pollock’s drip paintings [16], paintings of the Les Automatistes movement [17] [Fig. 8.(a)] and even some of Van Gogh’s [18] [Fig. 8.(b)] and Salvador Dalí’s [15] [Fig. 8.(c)], to name a few. Another domain where this technique might be useful for analysis is visionary art. For example, the shamanistic artworks of Pablo Amaringo [Fig. 8.(d)], inspired by the hallucinogenic brew called Ayahuasca. Equally, Roman [Fig. 8.(e)] or ancient Indian art [Fig. 8.(f)] analysis using this technique remains to be explored.

Fig. 8. Paintings can be analysed through the method of fractal analysis. (a) My Vertiginous Thoughts While I Contemplate From The Window by Eduardo Rojo from the Les Automatistes movement (courtesy https://www.saatchiart.com/). (b) Wheatfield by Vincent van Gogh (courtesy https://www.vangoghmuseum.nl/). (c) The face of War by Salvador Dalí (courtesy https://www.dalipaintings.com/). (d) Unicornio Dorado by Pablo Amaringo (courtesy https://pablo-amaringo.pixels.com). (e) 13th century, medieval art in the Basilica of Santa Maria in Trastevere, by Pietro Cavallini (courtesy https://www.planetware.com/). (f) Mughal court painting by an anonymous artist (courtesy https://asiasociety.org/).
  Since its development in the 1970s, the technique of fractal analysis has found employment in multiple disciplines of science and engineering. However, its implementation in the context of visual arts is a recent phenomenon and is envisaged to play a significant role in analysing artworks in the future. The fractal link between nature, abstract expressionist art and our neurophysiology still remain an incomplete story. Since its development in the 1970s, the technique of fractal analysis has found employment in multiple disciplines of science and engineering. However, its implementation in the context of visual arts is a recent phenomenon and is envisaged to play a significant role in analysing artworks in the future. The fractal link between nature, abstract expressionist art and our neurophysiology still remain an incomplete story.

Bibliography

1. D. E. Berlyne. Aesthetics and psychobiology. Appleton-Century-Crofts (1971).
2. Y. Güçlütürk, R.H.A.H. Jacobs, and R. Lier. "Liking versus complexity: Decomposing the inverted U-curve." Frontiers in Human Neuroscience 10 (2016): 112.
3. R. Taylor, B. Spehar, C. Hagerhall, and P. Donkelaar. "Perceptual and physiological responses to Jackson Pollock's fractals." Frontiers in human neuroscience 5 (2011): 60.
4. R. P. Taylor, A. P. Micolich, and D. Jonas. "Fractal expressionism." Physics World 12, no. 10 (1999): 25.
5. B. Spehar, C. W. G. Clifford, B. R. Newell, and R. P. Taylor. "Universal aesthetic of fractals." Computers & Graphics 27, no. 5 (2003): 813-820.
6. D. J. Aks and J. C. Sprott. "Quantifying aesthetic preference for chaotic patterns." Empirical studies of the arts 14, no. 1 (1996): 1-16.
7. S. Lakhal, A. Darmon, J. P. Bouchaud, and M. Benzaquen. "Beauty and structural complexity." Physical Review Research 2, no. 2 (2020): 022058.
8. J. R. Mureika, "Fractal dimensions in perceptual color space: a comparison study using Jackson Pollock’s art." Chaos: An Interdisciplinary Journal of Nonlinear Science 15, no. 4 (2005): 043702.
9. M. D. De Rios, and O. Janiger. LSD, spirituality, and the creative process: Based on the groundbreaking research of Oscar Janiger, MD. Inner Traditions/Bear & Co, 2003.
10. O. Janiger, and M. D. De Rios. "LSD and creativity." Journal of psychoactive drugs 21, no. 1 (1989): 129-134.
11. A. Hoffer, and H. Osmond. The hallucinogens. Elsevier, 2013.
12. M. M. Schartner, R. L. Carhart-Harris, A. B. Barrett, A. K. Seth, and S. D. Muthukumaraswamy. "Increased spontaneous MEG signal diversity for psychoactive doses of ketamine, LSD and psilocybin." Scientific reports 7, no. 1 (2017): 1-12.
13. Forsythe, Alex, Tamsin Williams, and Ronan G. Reilly. "What paint can tell us: A fractal analysis of neurological changes in seven artists." Neuropsychology 31, no. 1 (2017): 1.
14. C. D. Donderi, "Visual complexity: a review." Psychological bulletin 132, no. 1 (2006): 73.
15. A. Forsythe, M. Nadal, N. Sheehy, C. J. Cela‐Conde, and M. Sawey. "Predicting beauty: fractal dimension and visual complexity in art." British journal of psychology 102, no. 1 (2011): 49-70.
16. R. P. Taylor, R. Guzman, T. P. Martin, G. D. R. Hall, A. P. Micolich, D. Jonas, B. C. Scannell, M. S. Fairbanks, and C. A. Marlow. "Authenticating Pollock paintings using fractal geometry." Pattern Recognition Letters 28, no. 6 (2007): 695-702.
17. J. R. Mureika, and R. P. Taylor. "The Abstract Expressionists and Les Automatistes: A shared multi-fractal depth?." Signal Processing 93, no. 3 (2013): 573-578.
18. J. L. Aragón, G. G. Naumis, M. Bai, M. Torres, and P. K. Maini. "Turbulent luminance in impassioned van Gogh paintings." Journal of Mathematical Imaging and Vision 30, no. 3 (2008): 275-283.

  A traditional approach to compute the fractal dimension of a given image is the box-counting technique. In this technique the image is overlaid with a grid of identical square boxes of side length L. Then the number of boxes, N(L), that overlay with a portion of the image is counted (see Fig. 9). This process is then repeated over a range of different box sizes. Reducing the box size is equivalent to looking at the image with a finer magnification and capturing the higher spatial frequency components.

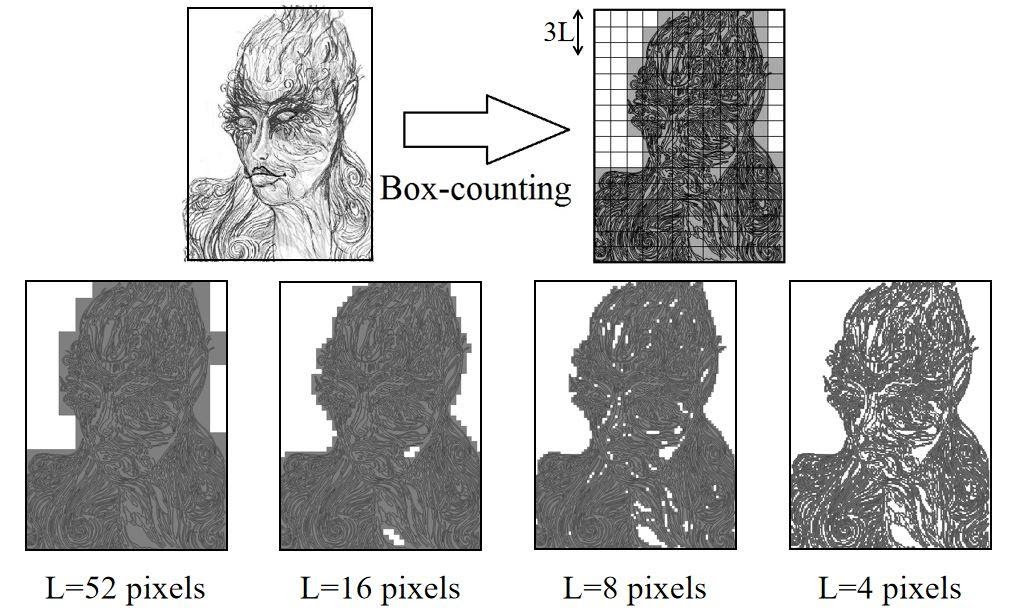Fig. 9. An illustration of box-counting of an image. The image on the top left was overlaid with a grid of square boxes of side length L. The boxes overlapping with the image are shown in grey and counted. Below, overlaid boxes are shown in grey for different box sizes.
  For a fractal, N(L) should scale according to the power law: N(L) ∼ L^(−D) where D is the fractal dimension. The negative exponent implies that on decreasing the box sizes, the image’s finer details are captured, and thus a larger number of boxes overlap with it. Thus D can be obtained by determining the slope of the straight line of the plot of Log(N) vs Log(1/L) of the considered image.

A science enthusiast, Debanuj finds himself studying optics and quantum mechanics after many rolls and knocks over the billiards board of life. He obtained a BS-MS degree in Physics from IISER Kolkata in 2017 and a PhD from the Paris-Saclay University in 2021. As a physicist, he believes in conservation.