Walking in Königsberg

Review

Debmalya Bandyopadhyay

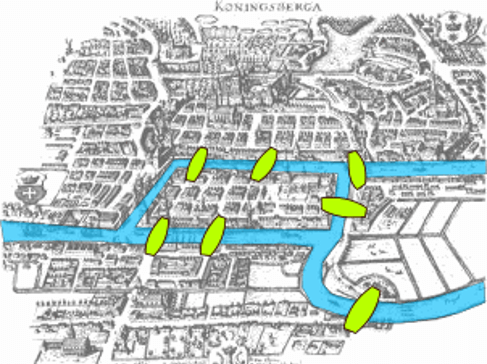
  We start our walk by the river Pregel flowing through the city of Königsberg (now Kaliningrad) in Prussia. Did I say Prussia? Yes, we are in the early 18th century, so Hitler isn't around yet, and we can safely concentrate on the question that has been maddening the citizens of Königsberg for a while! To get to it, let us first take a look at a rough map of the city.

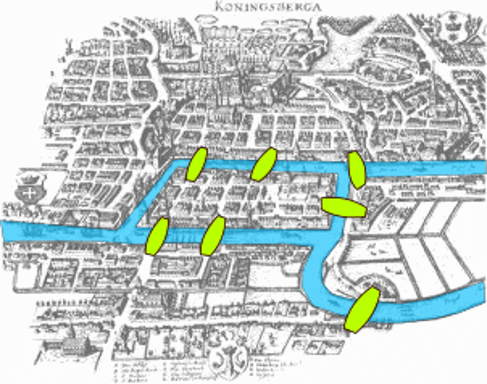
  Our object of focus in this map is the river that divides the city into four distinct parts as you can see. The green bean shaped objects are bridges that connect different parts of the city. Now the question that had been bothering the citizens for a while, was the following: Can someone start walking from any point in the city and end the walk having crossed each of the seven bridges exactly once ? Does such a route exist? The reader is hereby urged to try finding such a route in the given map themselves before reading the next part!

  The answer to this question was provided by the much revered mathematician (also physicist, astronomer, logician, geographer, engineer, you name it, he did it) Leonard Euler, one of the most magnificent human minds to have ever lived. In 1736, he published his solution to the problem, only proving that such a route does not exist! (My apologies to the reader) Surprisingly, in solving this problem he gave birth to the very exciting field of graph theory, the applications of which have infiltrated almost every aspect of our lives today.

  In order to understand Euler's simple solution, we shall arm ourselves with some very basic terminology. A graph is nothing but a set of points that we call vertices, and lines (called edges) each of which join two vertices. The following is an example of a graph whose vertices are marked A to G, with 12 edges.

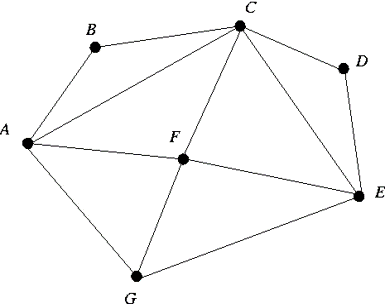
  Note that every combination is possible on a graph; we can have multiple edges between two vertices (called multi edges), we can have an edge going from one vertex to itself (called a self loop), we can even have directed edges that go from one vertex to another and not the other way back. The degree of a vertex is the number of edges that are touching that vertex. For example, in the above graph, vertex A has degree 4, and vertex G has degree 3. This is all the terminology that we need to tackle Euler's solution to the seven bridges problem.

  Now in his search for the aforementioned route in the map of Königsberg, Euler quickly noticed that the path that a traveller took inside any of the four landmass was irrelevant, the only thing that mattered was the sequence in which the seven bridges were crossed, since the constraint was placed on them. This insight helped him simplify the map significantly. All that mattered now were the bridges, and which parts of the city they connected.

  Euler represented the 4 parts of the city as 4 vertices, and the bridges as edges between them. In the above graph we denote this construction, with the left vertex representing the central island. The next observation was the most significant, that led to him concluding the non existence of such a walk.

  In terms of graph theory, we are required to start from any vertex on our graph, walk along the edges and stop at some vertex when we have covered each of the 7 edges exactly once. Now let us take a vertex that is neither our starting nor our stopping vertex. Then it must have an even degree, because we shall leave this vertex as many times as we enter it, and we cannot use an edge that we have already used before! So for such a vertex, the number of edges incident to it must be an even number. However, each of the vertices in the graph has an odd degree! (Three of them have degree 3 each and the vertex on the left has degree 5) Thus for such a walk to exist, no vertex can be a non-terminal vertex, meaning that such a walk cannot really exist with 4 vertices!

  Euler thus showed that the existence of such a walk only depended on the degree of the vertices and nothing else. He also showed that for such a walk to exist the graph had to be connected, meaning that one could traverse between any two of its vertices along edges, and that that the graph should have either 0 or exactly 2 vertices of odd degree. In the latter case our starting vertex (with one net outgoing edge) and ending vertex (with one net incoming edge) would be different, and in the former the walk would start and end at the same vertex. Carl Hierholzer later proved that this result was not only necessary for such a walk to exist, but was sufficient as well, meaning that for any graph satisfying these criteria, there would always exist such a walk! We now call such a walk as an Eulerian path, in honour of the great mathematician.

  Thus was born the field of graph theory, bringing one revolution after another with its applications. From modelling neural networks, understanding protein folding, optimizing traffic routes to designing the World Wide Web, it has been everywhere. Never did Euler judge the advances in technology his simple solution would bring along one day, and therein lies the beauty of human endeavour. What we drably dismiss as abstract, could very well assume form and define us tomorrow. After all, we are all slaves to our own brains!

Debmalya Bandyopadhyay is a third year undergraduate student pursuing Integrated BS-MS in Mathematics and Statistics from IISER Kolkata. Apart from math, he is likely to be found adrift in poetry, cinema and music.