Kolkata Connection with 2020 Physics Nobel Prize: The Role of A K Raychaudhuri

In 2020, Roger Penrose shared the Physics Nobel Prize with Andrea Ghez and Reinhard Genzel. If Stephen Hawking had been alive, he might have also won a share of the pie. Penrose, Hawking’s colleague at Cambridge University, got the prize for discovering that black holes are a robust prediction of Einstein’s general theory of relativity, a work in which Hawking was also involved. More generally, Penrose’s work involves the singularities of black holes.

In the 1950s, scientists were still trying to make sense of various solutions of Einstein’s equations, such as the Schwarzschild metric, the FLRW metric as well as the Reissner-Nordström solution, and the Oppenheimer-Snyder solution. Several cosmologists, including Einstein, were puzzled by the existence and nature of spacetime singularities in these solutions. A singularity refers to a point in spacetime where the equations of general relativity break down, and gravity becomes so intense that our current understanding of physics can no longer describe what’s happening.

Are these singularities an artifact of the assumptions of these specific models, or are they a generic feature of Einstein’s theory? It was in 1955 that a paper was published by a young physicist of Kolkata, Amal Kumar Raychaudhuri, that showed that these singularities were an inevitable consequence of Einstein’s gravity, independent of the symmetries of the model. This paper acted as the precursor of the 1969 paper published by Hawking and Penrose together, now famous as Penrose-Hawking Singularity Theorems.

Fig 1. The 2020 Nobel Prize in Physics honored Roger Penrose (left) for his work demonstrating that black hole formation is a natural consequence of general relativity, as well as Reinhard Genzel (center) and Andrea Ghez (right) for discovering a supermassive object—now understood to be a black hole—at the center of our galaxy.

Personal Life of AKR

In 1961, at Presidency University, a distinguished figure stepped out of a black ambassador car, dressed in a dhoti coat, white Punjabi, simple chappals, wearing thick glasses. If this had been Albert Einstein at the University of Berlin, the entire city might have come to a standstill. Amal Kumar Raychaudhuri, however, was approached by only a handful of his students and remained relatively unknown in Bengal and India despite his profound contributions. Fondly known as AKR among his students, his theory paved the way towards solving one of the deep problems of Einstein’s equations, and it even found its way into Stephen Hawking and Roger Penrose’s Nobel prize-winning work.

Born in Barisal, Bangladesh, on September 14th, 1923, A K R was the son of a mathematics teacher. His fascination with numbers began in childhood, and his numerical prowess gained notice day by day. He once proposed a solution to a math problem during an exam that surpassed the one the teacher gave. The headmaster was so impressed that he published the solution in the school magazine, giving due credit to AKR. While initially drawn to mathematics, he heeded his father’s advice and pursued physics instead. Graduating with a B.Sc. in 1942 from Presidency College and an M.Sc. in 1944 from Calcutta University, he joined the Indian Association for the Cultivation of Science (IACS) as a researcher in 1945. Here, he became interested in Einstein’s General Theory of Relativity. He conducted extensive research on the implications of Einstein’s theory, leading to the publication of his groundbreaking paper in 1955.

Fig 2. Dr. Raychaudhuri was born into a Baidya family from Barisal (now in Bangladesh) on September 14, 1923.

Einstein’s Theory of Gravity and The Problem of Singularities

Einstein’s general theory of relativity describes how gravity works as the curvature of spacetime rather than as a force in the classical (Newtonian) sense. Through these equations, mass tells spacetime how to curve, and curved spacetime tells matter how to move. For example, a planet orbiting a star follows a “straight line” in the curved spacetime around the star, but it looks like an orbit because the spacetime itself is curved. The Einstein field equations essentially link two essential things: the geometry of spacetime (how spacetime is shaped or curved) and matter and energy (what’s in that spacetime, like stars, planets, and energy fields). Karl Schwarzschild, a German physicist, made a groundbreaking contribution to general relativity shortly after Einstein published his theory in 1915. He found a solution to Einstein’s field equations that describes the gravitational field around a spherical, non-rotating mass, like a planet, a star, or, more famously, a black hole. Intriguingly, at the center of Schwarzschild’s solution, the spacetime curvature becomes infinite, meaning that the gravitational pull is infinitely strong, and matter is crushed to an infinitely small point.

Fig 3. In 1919, Arthur Eddington’s team confirmed Einstein’s General Theory of Relativity by observing the bending of light from stars near the Sun during a solar eclipse, with observations made in Principe (West Africa) and Sobral (Brazil). This groundbreaking discovery validated Einstein’s ideas about gravity and spacetime, propelling him to global fame.

In the following decades, theoreticians like Alexander Friedmann and Abbe Georges Lemaitre proposed their expanding universe models, which astronomical observations made by Edwin Hubble later corroborated. Their model used the well-known Robertson-Walker (RW) metric (independently obtained by Friedmann, Lemaitre, Robertson, and Walker). A metric describes the shortest distance between two points in any given spacetime. On a flat space like a sheet of paper, the shortest path is the straight line connecting the points, while on a curved space like the surface of the earth, the path will be longer because one must travel along the surface. The peculiar feature of these models was that they contained a point in time t=0, referred to as the Big Bang epoch, where the density and temperature become infinite. This was again a signature of a spacetime singularity, where the laws of physics would break down.

The presence of singularities in so many of these models is a dilemma: Are these singularities a consequence of the specific assumptions made in these models, or are they a fundamental aspect of Einstein’s theory in general? To get rid of these singularities, cosmologists proposed different ideas. One of them was the assumption of a spinning universe, where a centrifugal force would arise to prevent the collapse of matter at the axis, thus preventing the singularity. However, these models could not describe what was observed in reality.

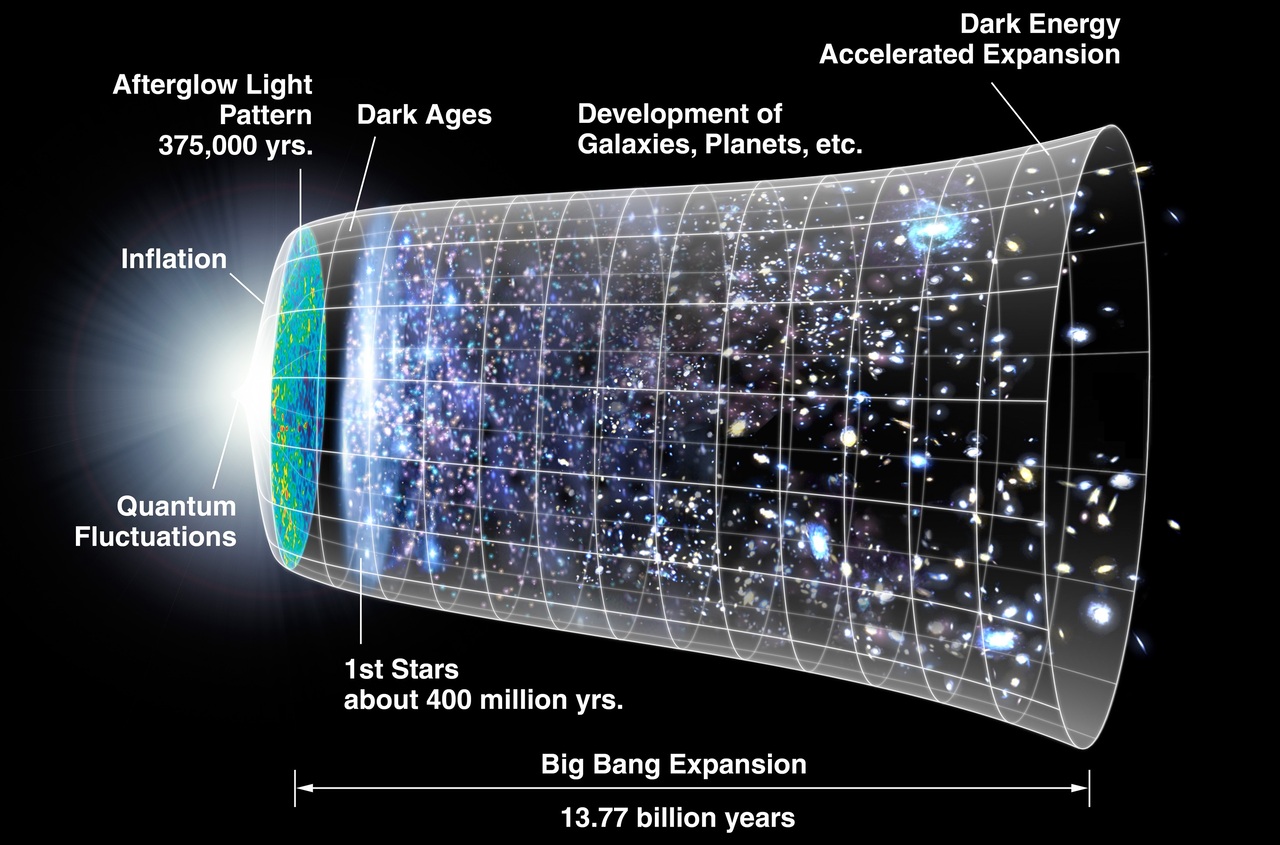Fig 4. The timeline of the universe’s expansion is illustrated with circular sections representing space, including hypothetical, unobservable regions, at each point in time. At the very beginning is the big bang epoch. followed by a rapid expansion during the inflationary epoch, while at the center, the expansion begins to accelerate.

The Raychaudhuri Equation and Penrose’s Nobel-winning work

A breakthrough was made in the problem of singularities by A K Raychaudhuri in 1955. He proposed a general equation, now named after him, which predicts the convergence of an endless stream of particles at a singular point governed by Einstein’s theory. This singularity exhibits infinite matter density and spacetime curvature. Because of the infinite curvature at the singularity, even light couldn’t escape from that point, and time ceased to flow. For the more interested readers, we write down the famous Raychaudhuri equation here

Fig 5. Trajectories of particles governed by Einstein’s equations can be thought of as a fluid moving through space. The Raychaudhuri equation describes how the area of the flow depends on various factors.

Even though the equation looks rather daunting, its physical import is apparent. It describes the motion of particles under gravity in the form of fluid-like flows. The paths of the particles can expand, contract, or distort, just like a fluid. The symbol $u_\alpha$ is a (four-)vector representing the velocity of particles moving in the presence of gravity. The quantity $\theta$, the main subject of the equation, is the divergence of the flow vector $u_\alpha$; it tracks whether the particles are coming into each other (converging, $\theta < 0$) or moving away from each other (diverging, $\theta > 0$). $\omega$ measures the rotation of the motion of the particles and is called the vorticity tensor. $\sigma$ is the shear tensor that describes the deformation of the flow paths. The derivative $\frac{du}{ds}$ measures the acceleration of the particles along their paths. $R_{\alpha\beta}$ is the Ricci tensor; it represents the curvature in spacetime compared to flat Euclidean space. As mentioned above, this curvature arises from the field equations of general relativity - mass tells spacetime how to curve, and curved spacetime tells matter how to move.

A spacetime singularity occurs when the divergence $\theta$ goes to infinity in either the positive or the negative direction. This can happen, for example, when the term with the Ricci tensor dominates over all the other terms. Since that term is typically negative, it will always drive the right-hand side of the equation to be negative and allow $\theta$ to flow to $-\infty$. Alternatively, if the spin term $\omega^2$ dominates over all the other terms, the right hand is necessarily positive, so $\theta$ then flows to $\infty$. Both of the cases lead to singularities. Singularities can be avoided if all the terms of the equation conspire to restrict the value of $\theta$ within a small neighborhood around zero; this requires terms of either sign to balance and compensate each other and fine-tune.

Fig 6. Flows moving under Einstein’s gravity undergo various distortions such as expansion, shear and rotation. The Raychaudhuri equation tells us how these changes affect the rate of expansion of the flow.

In summary, these considerations imply that singularities arise naturally in Einstein’s gravity, and this equation was later incorporated into the ‘Penrose-Hawking Singularity Theorems’. Thus, this equation, which Raychaudhuri derived to describe the behaviour of matter and spacetime near a singularity, provided a mathematical foundation for understanding the extreme conditions in such regions of the universe. The beauty of AKR’s work was that it presented, in a more general fashion, the mathematical formulation of the motion of a system of particles in spacetime. He also related his observations to singularity while studying Schwarschild’s solution. This equation paved the way for later research into the singularity problem. The Raychaudhuri Equation, with insights into the behaviour of matter and spacetime near singularities, was instrumental in shaping the mathematical tools and concepts that Penrose used in his work. Both Penrose and Hawking have acknowledged Raychaudhuri’s contribution occasionally in published papers and books.

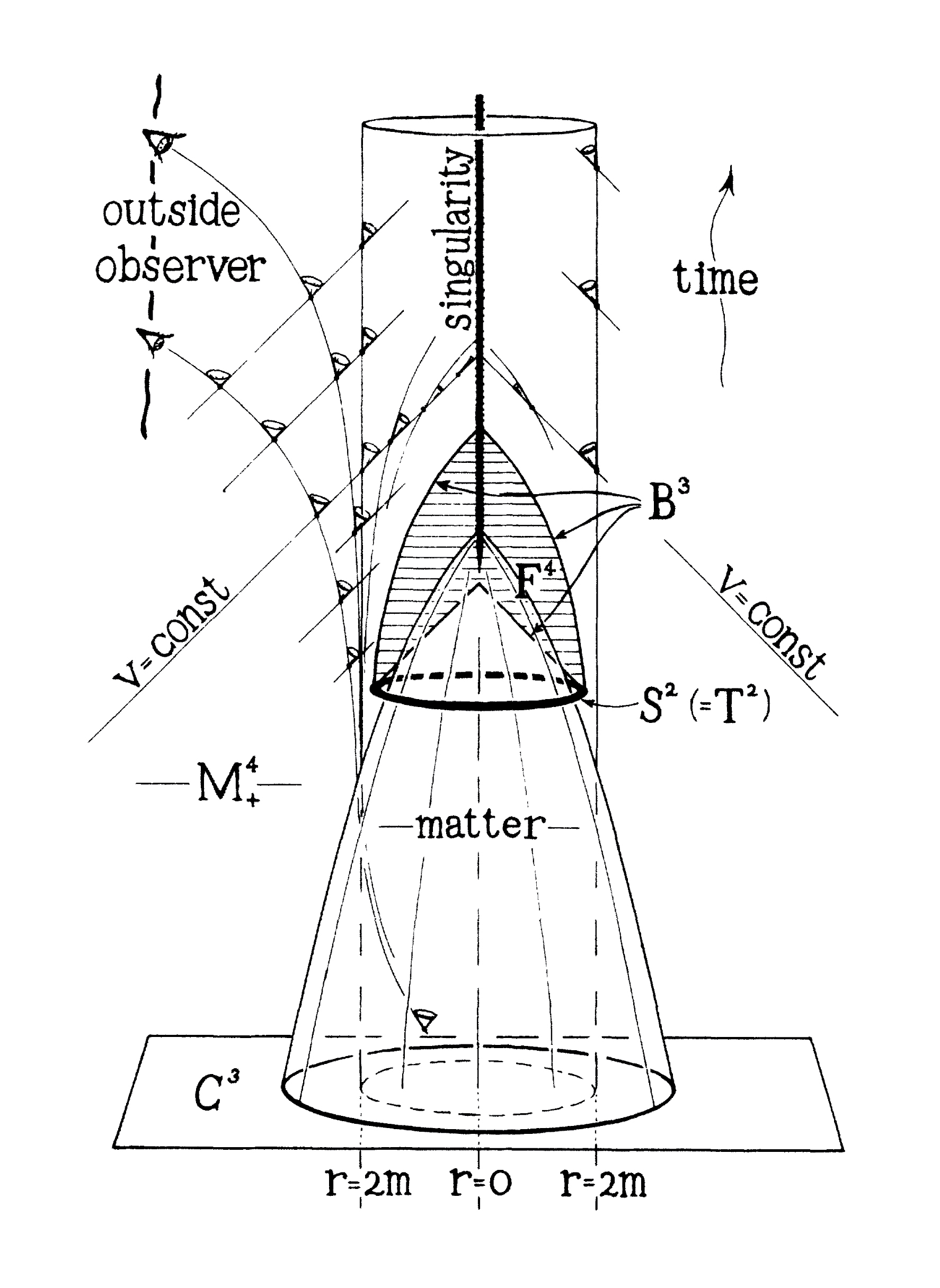Fig 7. In his 1965 paper, Penrose included this diagram to illustrate how matter undergoes gravitational collapse during the formation of a black hole. Time is represented along the vertical axis, while light rays travel at 45-degree angles, entering the black hole and continuing toward the central singularity. See [9].

The Lasting Legacy of AKR

Prof. Soumitro Sengupto, a former student of AKR and now a professor at IACS, remarked that Penrose always acknowledged his inspiration from Raychaudhuri. “AKR always set his research agenda, not motivated by what would likely bring him awards.” Prof. Narayan Banerjee of IISER Kolkata, another of AKR’s students, highlighted that AKR used geometry to identify a singularity where the laws of physics fail and physical quantities become infinite, specifically in the context of gravity and spacetime. Banerjee explained that this work laid the foundation for the Penrose-Hawking singularity theorems published in 1969. Banerjee also recalled being present when AKR first met Penrose at a workshop at Jadavpur University in 1987.

Fig 8. The Indian Association for the Cultivation of Science (IACS), founded in 1876 in Kolkata, is India’s oldest research institute, established with a focus on advancing scientific research and education. It was here that A K Raychaudhuri derived the groundbreaking Raychaudhuri equation.

In his later life, AKR continued to explore the problems of this type in general relativity. He also returned to the earliest problem of finding singularity-free models of the universe, which violated the singularity theorems of Penrose and Hawking. Later, with Naresh Dadhich, he published a paper where they obtained a singularity-free spherical model of the universe. On 6th October 2020, the Nobel committee announced that Roger Penrose had been awarded the Nobel Prize “for discovering that black hole formation is a robust prediction of the general theory of relativity.” While their press release explained that “Roger Penrose used ingenious mathematical methods in his proof that black holes are a direct consequence of Albert Einstein’s general theory of relativity”, his achievements were illuminated by the legacy of Bengali luminary Amal Kumar Raychaudhuri.

Fig 9. Prof. Narayan Banarjee (second from left) of the Department of Physical Sciences at IISER Kolkata being felicitated by Prof. Dhananjay Nandi (first from left), Prof. Rajesh Nayak (second from right) and Prof. Ayan Banerjee (first from right). Prof N Banerjee was a student of AKR during his time at Presidency University.

References