Spinning the world of physics into chaotic territory

Prajwal Padmanabha

   Complex systems are exactly as the name suggests, complicated. They are hard to understand and predict, and they are everywhere. This article talks about what makes them hard to understand and shows how scientists have overcome these difficulties, which led to them winning the 2021 Nobel Prize in Physics.

Tweet

  Let us start simple. You have seen a bird fly. It pretty much flies where it wants. Maybe if it is a pigeon in Old Delhi, it flies towards seeds thrown by a kind human. Sometimes, you might see two or three birds flying together in formations that you'll find fascinating. On rare occasions, you might even see 10-15 birds flying in a striking formation, and you pause to appreciate the beauty of nature.

  If you are in a contemplative mood, you might wonder why they fly in a formation. This is where the real beauty appears. Thousands of tiny birds called starlings manage to fly in these incredible swarms that look like they are all being controlled by a supervillain from the comics. Somehow, these groups of thousands of individuals manage to coordinate and pull off this amazing feat. Even more surprising is that this is not just limited to birds! If you observe closely, you will see this everywhere– in the oceans, on land, in the air, and even at microscopic levels where they amazingly communicate through chemicals. The contrast here is that you are unlikely to observe these patterns if a single or few individuals are left on their own. This is what lies at the core of complex systems! But this is also what makes complex systems hard to define.

A swarm consisting of thousamds of individuals (Photo by James Wainscoat on Unsplash)
  Whenever physicists talk about complex systems, there is no precise definition that everyone uses. This is because we do not yet have an exact idea of what makes something complex. Defining complexity is made harder because there are different properties of systems considered to be complex, which may or may not overlap between two different systems. [ref] In some instances, complexity might arise from the number of variables needed to describe the system. In others, it might be a behaviour that emerges only when a group of particles are present. In some cases like the weather, a slight change in the system might lead to large changes down the line, which is called chaotic behaviour.

   While there lacks a single definition of complex systems, there are specific properties that occur commonly in systems considered to be complex. These properties are key to understanding a system.

  One of the top features of complexity is emergent behaviour, like the one described at the beginning of the article. Phenomena that are absent while dealing with a single or a small number of components might be visible with larger numbers. These systems show collective behaviour in some ordered fashion and parameters usually control this behaviour. In models of swarming, this is randomness in the movement of birds. In physical systems, ordering is generally controlled by temperature. Transitions from disorder to order are some of the most important areas of study, which we will discuss again after looking at some more features of complexity.

   Complex systems are also typically nonlinear. A linear system is one where the effects are proportional to the change a system experiences. Newton's laws of motion are a good example of the linear effects of the force on acceleration of a body. But a complex system might exhibit nonlinear effects, which also ties in with the idea of chaos. An example of this could be two pendulums connected to each other. We pull any one of them to a certain point, release it, and then observe the positions of the two pendulums. If this is a lab experiment, we would repeat it to verify that what we recorded the first time is correct. But now, if we accidentally shift the initial position of the pendulum even by a tiny bit, the resulting positions are very different! A tiny change in the initial position leads to a disproportionate change in the later position. This is an example of a nonlinear effect. This effect is commonly known as The Butterfly Effect, referring to how a flap of a butterfly's wing could lead to a hurricane at some point down the line.

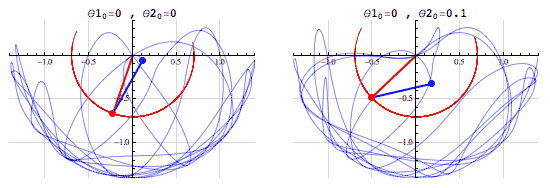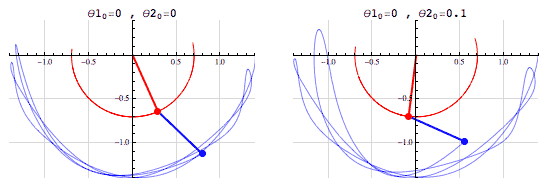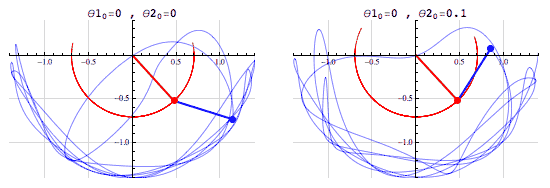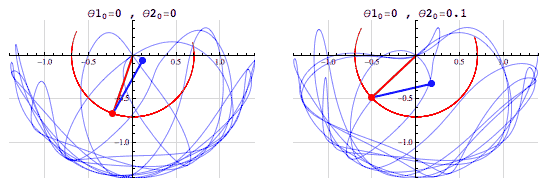Chaos shown by the double pendulum with a slight difference in the starting angle of one of the pendulums. The paths are seen to be very different, especially at long times. Image: Fouriest Series, CC BY-NC-SA 4.0
  Another essential aspect of complex systems is critical transitions. Transitions, as discussed earlier, are changes in the state of the system, the most common example of which would be ice melting into water or water boiling to vapour. While transitions can be of many kinds, these are called phase transitions. The disorder to order phase that we discussed earlier is another kind. In our example of water boiling, we could measure the temperature and see that it increases steadily and then predict when the water would start boiling. But in the case of complex systems, it can usually be abrupt without any warning signatures. The origin of this can lie in many factors, like the number of elements in the system, the number of parameters that one would need to describe the system with a model, incomplete knowledge of all the system's processes, and so on. But such abrupt transitions are of great importance and are called critical transitions.

  A frequent characteristic of complex systems is memory. While this might seem strange, a lot of physical processes are memoryless. An appropriate example for this would be to consider a drunk person on the streets of Paris. While the person is an inherently biological system, they might very well serve as a physical particle, for our example. This person has forgotten where they have come from and wanders around the streets to find their home. You take a map of the city and start marking where the person goes, and as expected, you notice that they are wandering aimlessly. Try to think if they are moving in a particular direction and take their average position. You notice that all their wanderings are centred around the bar they exited from! This doesn't give you any information, so you try to see how far they are exploring on average. You can mark the absolute distance from the bar while ignoring the direction. But an easier way to do this is to take the distance travelled squared since it will be a positive number. You notice a particular pattern here ‒ the longer they wander, the larger "area" they explore. This average displacement squared varies linearly with time. There is no memory associated with this example because it is inconsequential, at what time the person exited the bar initially. But complex systems frequently retain memory! The time at which you start or the parameters of the system at a particular instant become important. Suppose the person is not drunk enough and remembers the positions they visited to find their way. In that case, it instantly adds memory into the system, making it much harder to calculate quantities as we discussed. Complex systems sometimes have many such particles that retain memory, with the particles interacting between themselves. There are many other features of complex systems that can be described, but the ones mentioned are some of the most frequent ones.

  While the discussion on complexity and the different properties are not strictly necessary to understand the work of the Nobel laureates, it is demonstrative of how difficult the study of complex systems is. It helps us appreciate the breadth of phenomena covered by the systems. Giorgio Parisi's work fits in the context of what we have discussed. His contributions to physics range from working on subatomic particles to the theory of fluid dynamics. The Nobel Committee's message for the prize reads- the award has been given to Giorgio Parisi "for the discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales." [ref] Specifically, the prize refers to his work on systems called Spin Glasses.

  To understand this, let us consider a magnet. You remember that the North pole of a magnet attracts the South pole. Now imagine magnets pointing in different directions on a sheet of paper. Instead of laying flat on the paper, they point upward towards different points. These magnets are called spins. Sometimes, spins like to point in the same direction as their neighbour and sometimes, they like to point in a completely opposite direction. The first kind of interaction is called ferromagnetic interaction, and the latter is called antiferromagnetic interaction. It is also possible that the spins are ferromagnetic in one part of the sheet while antiferromagnetic in another. When this happens, all the spins cannot be pointing in the same direction and constitutes what is called a disordered system.

  Imagine three spins on three points of a triangle, all preferring to be antiferromagnetic. If the first spin points up, the second spin would point down. But the third spin is in a conundrum. It cannot point up or down because it would be violating antiferromagnetic preference with one of the neighbouring spins if it does so. This is called frustration because the third spin is frustrated with its condition.

  Spin glasses are essentially frustrated disordered systems. Each orientation of the spin will have a certain energy, and if the spins are frustrated, their energy increases. Physical systems left on their own always like to have minimal energy. They are like us on a lazy winter morning. Because of this, in a frustrated disordered system, there is no single set of orientations of all the spins on the sheet that would have the least energy. Instead, there are multiple possibilities where the system is frustrated but with the same energy. All these possibilities are disordered by nature, with spins pointing in wildly different directions.

  Let us consider the example of ice to water transition again, but now in reverse. If we lower the temperature of a water tray, it gradually becomes ice. The state moves from a free-flowing liquid to a rigid solid. The order of the system increases because, in ice, the molecules of water are arranged in a very predictable manner. The temperature is called the order parameter because it controls the order of the system.

  Because of the very nature of spin glasses, it is not easy to tell if a system is in a particular configuration, either due to low temperature or the inherent disorder in the system. Giorgio Parisi employed a trick called the Replica Method. As the name suggests, it looks at two possible orientations of all the spins and considers how much they are a replica of each other. By looking at all possible pairs of orientations, he defined a new order parameter that helps us to know when the phase transition happens in spin glasses.

  Spin glasses are used in a variety of fields [ref]. Some of the few examples are computer science, optimisation problems, finance modelling, biological evolution, and the mechanism of protein folding. Considering the wide-ranging applications of the theory, it is no surprise that a breakthrough in it has been awarded one of the most prestigious prizes in physics.

  The second half of the Nobel prize has been awarded jointly to Syukuro Manabe and Klaus Hasselmann "for the physical modelling of Earth's climate, quantifying variability and reliably predicting global warming".

  Before beginning, some distinctions need to be made between climate and weather. While climate constitutes long term patterns, weather is shorter and is subject to more fluctuations. Since prehistoric times, we have tried to predict both the climate and weather for agriculture and other purposes. But climate models started in the 19th century when wind patterns were mapped, and scientists began looking for explanations of it based on simple models of heated spheres. As time progressed, more complicated models that took into account more variables and parameters started to appear. But, the climate is a chaotic system. Even the simple models of weather and climate show chaos. Naturally, it is expected that the real system is also chaotic. The system is also quite nonlinear making modelling difficult.

  Syukuro Manabe considered a vertical column of air and mapped the flow of carbon dioxide within that column. He accounted for different processes and variables that have interplay between them. The result of those models? An estimated 2.3 degrees increase in global temperature when the carbon dioxide concentration doubles. It is impressive to note that the estimate Manabe and his collaborators gave in 1967 was with a computer with only 5 Mb of RAM and still remains accurate! [ref]

  Weather, on the other hand, is short term fluctuations. Klaus Hasselmann considered climate to be an evolution of these short term fluctuations over a long time. He incorporated the random walk example we saw into the coupling between climate and weather, resulting in a simple set of equations that anyone could easily use. The general idea of including randomness into climate modelling led to stochastic climate modelling as a field. In particular, Hasselman was able to connect his predictions to observations with stochastic climate models. Once the predictions match the observations, it is possible to look at the model and change parameters. Specifically, he was able to separate natural and human causes to changes in temperature. His work conclusively showed that the increase in temperature of Earth's atmosphere is due to human activity! [ref]

  In today's "climate" of misinformation and fake news, it is necessary to have concrete research that attributes the effect of increasing emissions and linking human activity to rising temperatures. Manabe and Hasselman's work does precisely this and provides a base to develop further intricate models to capture more phenomena. Considering the long term impact of their research, it is not surprising that they were awarded the Nobel Prize.

  Moore's law predicts that every year, computing power doubles while sizes of computers halve. Though we might be nearing the end of validity of this law, it has certainly proven to be accurate in the last few decades. Complex systems scientists have utilised the eruption of modern computing power immensely. This is especially true when the models need to incorporate multiple parameters and variables. The field of complex systems is truly interdisciplinary. It manages to use tools from mathematics to build physical models that are applicable in biological fields

  Moving forward, it will be possible to understand more complex phenomena. The device you are reading this article on is more powerful than anything we used to put humans on the moon. Standing at the precipice of this significant change, we would not be able to see the far-reaching impact of what new science will bring us. Going back to safe global temperatures may not be as simple as lowering emissions and is likely to need more drastic measures. The knowledge to answer these questions and chart a path to navigate these troubled times can only come from more information about these systems. The recent Nobel prize will surely motivate more young researchers into the field and lead to unlocking more secrets of the beautiful world around us as long as we preserve it.

Prajwal Padmanabha is a PhD student in Physics trying to understand the applications of statistical physics to biology. Hopefully, by the end of it, he understands something at least.