Hilbert’s Quarantine Centre: To infinity and beyond!
Review
Debmalya Bandyopadhyay

This article revisits a classic thought experiment in Mathematics. It explores some of the intricacies of countable infinity and how its definition can be used to achieve seemingly impossible results, and contemplates how useful these results may be in the current pandemic.
Tweet
While I write this sitting in the privilege of my home, the pandemic keeps raging outside, the hunt for a vaccine continues, and the number of active cases keep skyrocketing towards the figures in Buzz Lightyear’s memorable line, “To infinity and beyond”. As health departments around the world scramble to find space for isolating potential victims of the virus, perhaps it is time to turn to math for possible solutions, or rather to a curious thought experiment developed by one of the most fantastic German mathematicians to have ever lived- David Hilbert himself.
Hilbert was one of those prolific polymaths who emerged towards the end of the 19th century. His genius was everywhere and in abundance. He had made contributions in not just a number of mathematical disciplines, but he also built the fundamentals of mathematical logic itself - a field of study now known as ‘proof theory’. He kickstarted several arenas of research by presenting a collection of 23 unsolved problems in the year 1900, that kept mathematicians busy throughout the last century. After 120 years, only 9 of these problems have well agreed solutions, some of the others have solutions which are only partially accepted in the mathematical community and some (including a cheeky little question called the Riemann hypothesis) remain unsolved to this date.

Figure 1: David Hilbert
But fret not, we would not be discussing any of those problems in this article. We would much rather focus on the pandemic at hand, and explore a hypothetical quarantine centre which can not only hold an infinite number of residents, but (with a little belief in Buzz Lightyear from Toy Story) something far beyond that number.
Hilbert had introduced this idea in a 1924 lecture, and it was later popularized by George Gamow in his book “One Two Three...Infinity”. This paradox is popularly referred to as “Hilbert’s infinite hotel” or “Hilbert’s grand hotel paradox”. Since the current pandemic disallows us the luxury of a hotel and we have lives to save, we shall adopt its structure to that of a quarantine centre. But before we jump onto the jaw dropping properties of this place, let us first explore a little about what infinity really means.
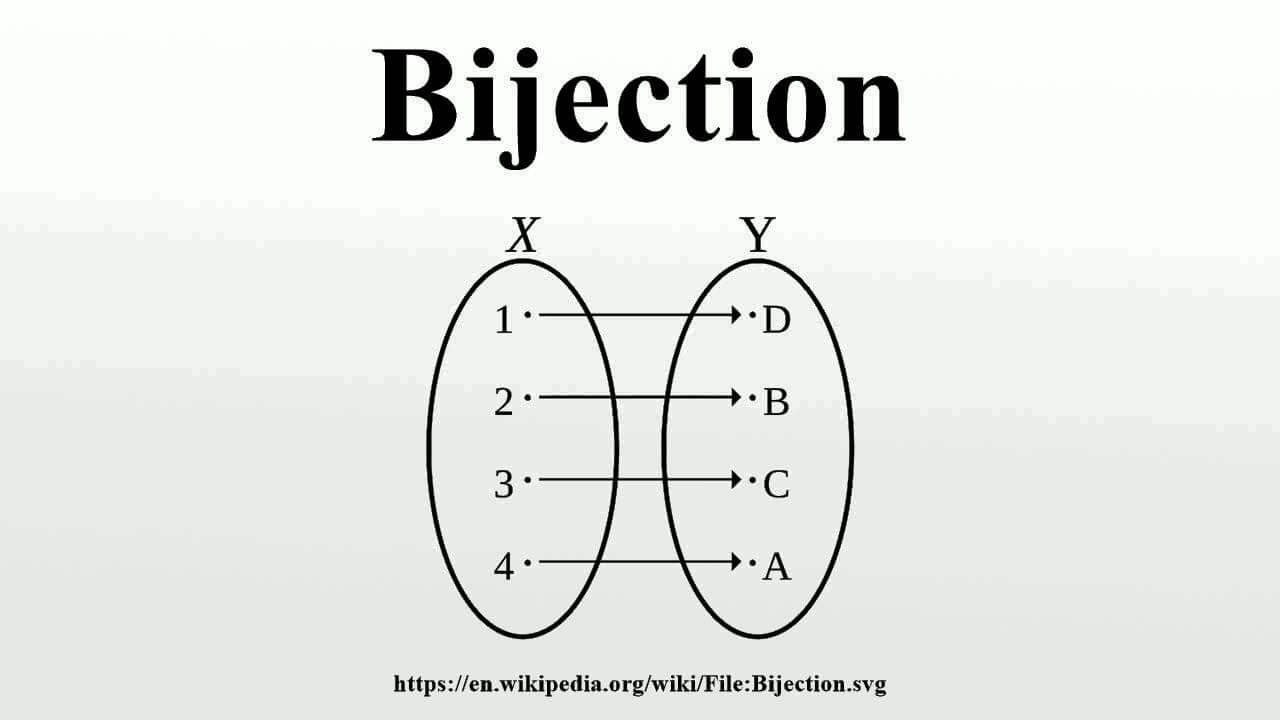
Mathematics mostly deals with two kinds of infinities, one countable and the other uncountable. For most practical purposes the concept of a number being infinite is understood as something which is unbounded, or greater than any finite number one can imagine. When the cardinality (fancy term for number of elements) of a set is said to be countably infinite, it means that we can establish a one to one correspondence between elements of the set, and the set of natural numbers. This basically implies that for each natural number we can identify a unique element of the set such that no element in the set is left unidentified. Thus we can count the elements of the set (even if there are infinitely many of them) using our natural intuition for counting and that is where the name comes from. This unique correspondence between two sets is called bijection. As an example, a bijection between the set of all positive integers and the set of all negative integers is f(x) = -x.
On the other hand, uncountable infinity is something far larger and messier (like the set of all real numbers) and we cannot count them because given any element from an uncountable set it is impossible to determine its immediate successor or predecessor in the set. (As a small example for the real numbers, one might think 0.51 comes right after 0.5, but then 0.501 sits in between them, contradicting the thought!). The cardinality of an uncountable set is thus strictly greater than the set of natural numbers, and one cannot establish a bijection between the two. (John Green had probably meant this when he wrote “Some infinities are bigger than other infinities.”) To save ourselves from mental exhaustion, for the rest of this article we will be dealing with and referring to only countable infinity, which is well behaved and kind enough to allow us tricks that we would use here.
Now, consider the set of even natural numbers. This is a strict subset of the set of natural numbers. In spite of this, it turns out that one can establish a unique correspondence between it and the set of natural numbers (with n corresponding to 2n)!
How is it possible that the cardinality (or size) of a set is the same as that of another which is entirely contained in it? As an equally surprising result, it turns out that the set of all integers (positive, negative and zero) which strictly contains the natural numbers, has its cardinality same as that of the natural number set itself! There is nothing wrong with this apparent contradiction. The way we defined our (countable) infinity, our infinite sets may hold subsets that are also the same size as that of natural numbers. Hence, well defined bijections are completely possible between a set and it’s subset, if both are infinite. In fact, any infinite subset of a countably infinite set is bijective to it because both are bijective to the set of natural numbers.
Thus, the following sets have the same cardinality (size) : Even natural numbers, odd natural numbers (since they only differ from the evens by 1), natural numbers, and integers, for we can establish bijections between any two of them! One can also prove that countability is preserved under (countable) unions and finite cartesian products, a fact we would use later on. (Finite cartesian product of a set with itself (in our case, the set of natural numbers since we are only concerned with cardinality) can be thought of as taking finitely many layers of the same set at the same time.) Mathematics is indeed a land of strange miracles, and we will unearth stranger phenomena in this article itself!

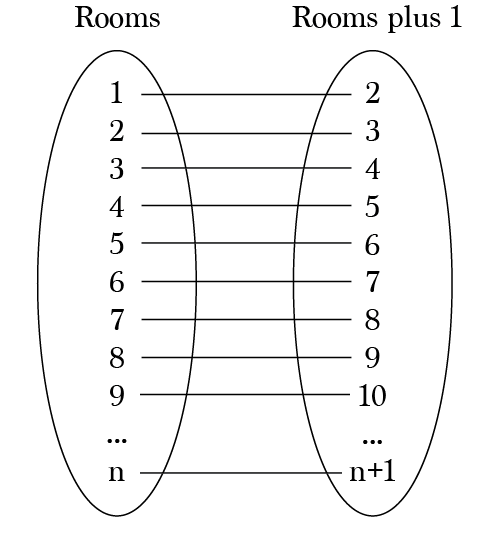
Now that we are somewhat versed in the basic definitions, it’s time to visit Hilbert’s quarantine centre, which (as you must have guessed already), has infinitely many rooms. For ease of understanding we shall name the rooms as 1, 2, 3 and so on with natural numbers. On a given night, say we have a full house, and a suspected patient arrives asking for a room. For any other quarantine centre, we would have to turn the visitor away, but we don’t do that here. Even though we have a full house, all we need to do is to shift the occupant of room 1 to room 2, that of room 2 to room 3, and so on.
Thus by shifting the occupant of room n to room n+1, we free up room 1 for our new guest. But doesn’t this mean that the person who resided in the last room would be thrown out? That is precisely the catch, because in this quarantine centre, there is no last room! There is always a next room to any given room, but since there are infinitely many of them, there is no end to them. Thus you know what to do if any ‘finitely many’ covid suspects arrive, say k many of them. All we need to do in order to find them space is move the resident of room n to room n+k, freeing up the first k rooms for our new guests in the process.
But on a particular night, the government’s worst nightmare comes true, and a coach of infinitely many covid suspects arrive at our quarantine centre. Instead of vilifying whoever sent them together in a single coach, we need to quickly arrange rooms for them in our centre. Now we will take advantage of the weird fact I mentioned earlier. All we need to do is move the resident of room n to room 2n, thus moving the entire set of natural numbers to the set of even natural numbers (since their cardinalities are the same!) freeing up all the odd numbered rooms in the process. Since the set of all odd natural numbers also have the same cardinality as that of natural numbers, we have no trouble with assigning rooms to all of our new guests.

But due to the exponential growth rate of infections, soon the situation gets even worse sending the government into a blind panic attack, and we are sent an infinite number of buses, each carrying infinitely many suspects. This is a situation none of us were prepared for, but we have to somehow accommodate all of them in our quarantine centre. We turn to the natural numbers that mark our rooms for a solution, to find a way to pull off this apparently impossible task, and a very special set of numbers called the prime numbers come to our rescue.
We first claim that the set of all prime numbers is infinite. If primes were indeed finite in number, we could have taken the product of all the primes, added 1 to this product and formed a “new” prime, because no prime (hence no number except 1) can divide its own multiple and an immediate successor of that. Thus by comments made earlier they are also of the same size as the set of all natural numbers. Moreover, no prime interferes in another prime’s powers (for example, no power of 2 is divisible by any other prime other than 2). Hence for each prime, we have an infinite chain of rooms which are its powers. Voila!

We first move our existing set of residents to rooms which are powers of the first prime, 2. Once this is done, we take the first bus and move its infinite number of passengers to rooms that are powers of the next prime, 3. For the second bus, we consider powers of the next prime, 5. Since both the set of all primes and the set of all possible powers of each prime are the same size as the natural number set, we have no trouble in accommodating infinitely many buses each filled with infinitely many passengers!
What is even more surprising is that once we have moved all the people into their rooms, we have also vacated infinitely many rooms, because any composite numbered room that is not a power of a prime is now vacant! Note that this is not the only way to accommodate these many people. There are other ways to assign them room, for example we could have assigned the person in the ath seat of the bth bus the room 2a3b (after moving our existing residents to the room numbers where b=0 in the above formula). Since prime factorization of any natural number is unique, no two persons would be allotted the same room and we would have infinitely many rooms vacant in this case as well.
We can similarly adapt our above algorithm(s) to a situation when we are sent an infinite number of ships, each carrying an infinite number of buses, each of which carries infinite passengers (The government has basically given up at this point, all hope is lost, except that of mathematicians). We now have 3 layers of infinity, but we don’t get intimidated by such figures anymore. All we have to do to fit this enormous amount of people is raise our prime powers as powers of another layer of primes. If that confuses you, think of it as assigning the person in seat a, of bus number b, of ship number c the room papbc where pa and pb are the ath and bth primes.
If we want to extend the alternate method that we described above, we move the person seated in the above mentioned way to room number 2a3b5c. We can keep adapting the procedure(s) similarly as long as we have finitely many layers of infinity, because finite cartesian products (or layers) of countable infinities are countable infinity in return, and as long as we have our set of guests to be countably infinite, we can find them rooms in our quarantine centre. Unfortunately, the same is not true if we have countably infinite layers of infinity, because it can be proved to be uncountable- the other dreaded infinity where none of this wholesomeness is preserved.
Of course, we are only assigned the task of planning who gets what room, and we leave the other details to the staff. We need not worry ourselves about moving possible patients in and out of rooms, changing their allotment almost every other night and ensuring safe distancing and sanitization in the infinite corridors. We also leave the task of building this architectural marvel to our engineer friends, and once they are done we can use our math to save the world. If you know someone who might be up for the job, make sure you send them some motivation with this article and a copy of Toy Story!
References
Debmalya Bandyopadhyay is a fourth year undergraduate student pursuing Integrated BS-MS in Mathematics and Statistics from IISER Kolkata. Apart from math, he is likely to be found adrift in poetry, cinema and music.
signup with your email to get the latest articles instantly