Is Geometry Disconnected From Algebra? An excerpt from 1984
Review
Satwata Hans
Tweet
In our early days in high school, geometry and algebra seldom showed any deeply rooted connections. When we first learn about geometry, it is introduced through the techniques used by the ancient Greeks from the school of Euclid of Alexandria. In this realm, we use exclusively geometric arguments to study its properties. Later, when we look at conic sections (parabola, ellipse, hyperbola), our approach is to solve algebraic equations. For the first time we see a link between these two subjects. Today, we look at a case where a beautiful geometric entity arises solely from an algebraic object. Luckily, our problem at hand will be reasonably simple and charming. But in modern mathematics, mathematicians often turn towards studying complicated algebraic objects using their geometry. This is the famous field of algebraic geometry.
So with this mathematical motivation, walk with me to the dystopian land of Oceania. News has spread that it is in dire need of a city planner. The kingdom of Oceania has three mansions for “Big Brother” to reside in, and three official buildings – Ministry of Peace, Ministry of Truth and the Ministry of Love. All these six structures are close to each other, but their connectivity isn’t great. Imagine that the three residential buildings form a triangle, and the three Ministries are in the mid-points of the sides of this triangle, respectively. The only roads here are the sides of the triangle, while the interior of the triangle has a dense covering of greenery. Big Brother wants a new highway connecting all the Ministries, but without passing through the residential mansions. Furthermore, anyone undertaking the job has to keep in mind the environmental consequences of cutting down trees. The reward, however, is a hefty sum of 1 million dollars.
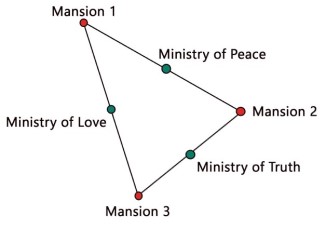The first architect to approach Big Brother proposed creating a triangle of highways with the vertices being the Ministries. Big Brother was infuriated at this plan, labelling this man as having no sense of aesthetics and sentenced him to a lifetime of forced labour. People were now scared to approach him, wary of dangerous repercussions if things didn’t go according to plan. However, this didn’t faze the head of Central University of Oceania, Marden Junior. He formulated the architecture in terms of a simple mathematical problem and solved it using complex numbers and a little geometry.
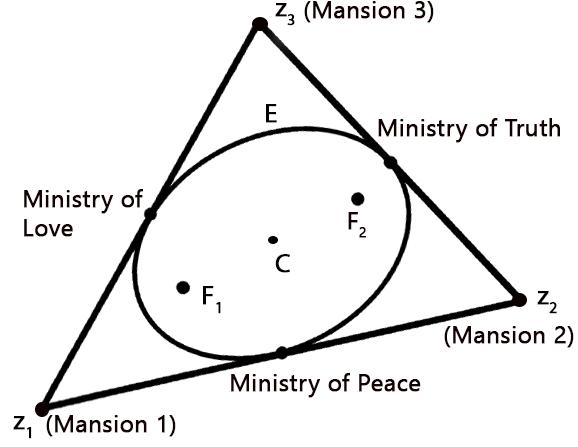
Marden labelled the coordinates of the three residential mansions as {z1,z2,z3}. What he did next was the most non-trivial part. He considered the complex polynomial p(z) = (z-z1)(z-z2)(z-z3) and showed that the design of the highway depends entirely on this polynomial.
Let us first understand what this beautiful result says. As we started out with a cubic polynomial, let us turn to something simpler — its derivative. The derivative of a polynomial is just the rate of its change of its output with respect to a change in its input. Now the derivative p'(z) is a quadratic polynomial, and enthralling us, this only has two roots! Marden focuses on these two devils and chalks out two cases — when the roots are unequal and when they are equal.
In the first case, he claims that there is a unique ellipse with those precise roots as its two foci. But that's not all. The three sides of the triangle are also tangent to this ellipse exactly at their midpoints, which are the three Ministries! If that sounds hard to visualize, I have a pretty picture for you.
What happens when the two roots are equal? You guessed it right- the ellipse becomes a circle, and the (equal) foci are now its centre. The sides of the triangle are still tangent at exactly the midpoints. The reader would like to pause for a moment and think here — that as the ellipse-shape shifts into a circle, the foci come uncomfortably closer and closer to the midpoint, until they are the same point! This is where one learns that a circle is just a special case of an ellipse.
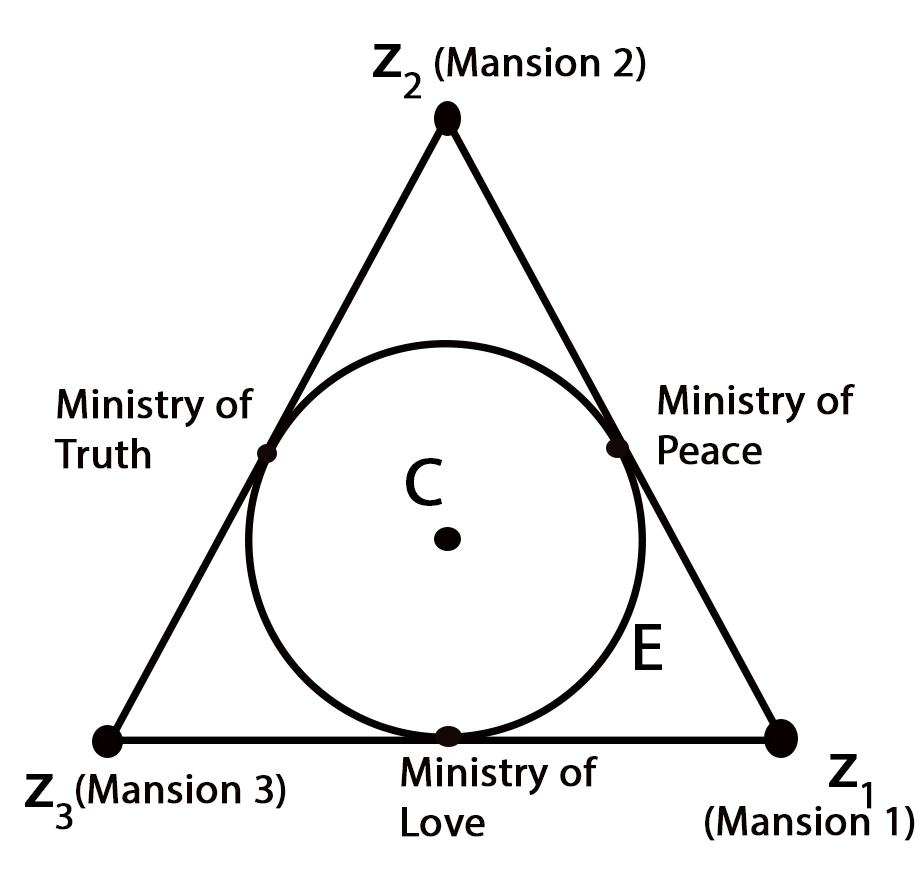But Marden didn't just stop there. He goes a step further, into the double derivative of p(z), which (to our sheer delight!) has only one root. He says this root is precisely the centre of this ellipse/circle and also the centroid of the triangle. Depending on the roots of the derivative, either the ellipse or circle will be the desired new road between the three Ministries. An ellipse/circle inscribed in a triangle would look beautiful from an aerial photograph and also requires very few trees to be cut down. Big Brother was thrilled at this plan and awarded the “Order of Humanity” to Marden, the highest honour a civilian could get in Oceania. He even saw some further scope in this architecture and ordered his statesman to build a statue of himself at the centre of the ellipse/circle. This would be the tallest statue in the world, called “The Statue of Equality”.
Now the results stated above might seem a little intimidating as it asserts a lot of things. To slowly gain some insight into Marden’s solution, we wish to start with the easiest part - the last conclusion. Our desired complex polynomial was p(z)=(z-z1)(z-z2)(z-z3) . The double derivative of p is p''(z)=6z-2(z1+z2+z3). Hence, the only root of p''(z) is (z1+z2+z3)/3, which is indeed the centroid of the triangle and the spot where a statue of Big Brother will stand.
Now comes the time to see the crux of Marden’s genius and make the problem one step simpler. Given a triangle and an ellipse inscribed in it, if we rotate, translate, stretch or squeeze the whole figure, all the above-stated results remain unchanged. Thus, to make the problem more accessible, we can reorient the figure and conveniently adjust its size. In technical language, this transformation is called an affine transformation. This figure can make it simpler.
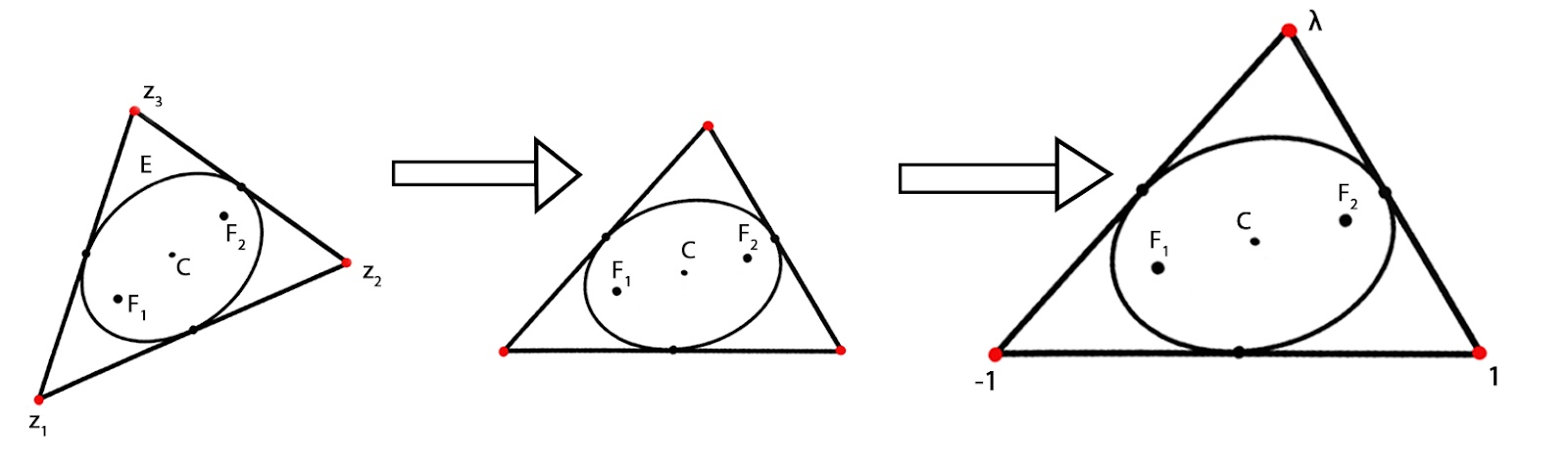To argue why these results are indeed true, we first use an affine transformation such that the three mansions lie on the co-ordinates {1,-1,λ} with λ lying above the X-axis. Now if λ1, λ2 are roots of p'(z) we can construct an ellipse with the two foci as {λ1, λ2} and passing through the origin. It will follow from a simple calculation that both the lines joining the foci and the origin (λ1O and λ2O respectively) subtends equal angles with the X-axis. By property of ellipses, this is only possible for a tangent line. So let’s summarise what we have argued - the side with vertices {-1,1} is tangent to this elliptical path precisely at the midpoint, which in this case is the origin O.
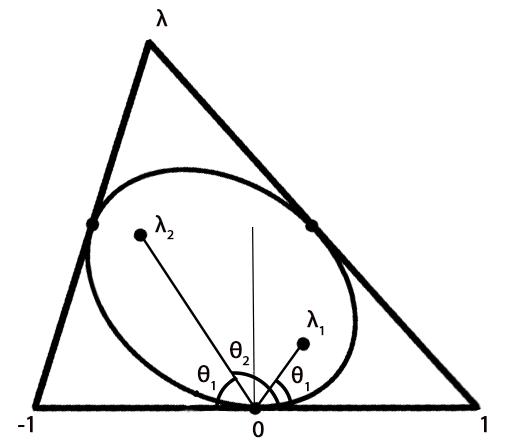We have already shown that one side is tangent to this ellipse at the midpoint. If we can somehow show that the other two sides are also tangent to this ellipse at their midpoints, we are done.
Resorting back to our trusted friend, we use an affine transformation again, now considering the triangle with vertices {0,1,λ} where lies above the X-axis. Again, if λ1, λ2 are the roots of p'(z), we have already seen that there is an ellipse which has foci λ1, λ2, and is tangent to the X-axis (or the side with vertices {0,1} ) at ½. Now the origin O lies outside the ellipse and we can draw two lines from it which will be tangents to this ellipse. One such line is already the X-axis, and again a tedious calculation will show that the other tangent line is indeed Oλ. This is exactly the second side of the triangle. Furthermore, it will follow from the angle relations that the point of tangency is the mid-point of this side.
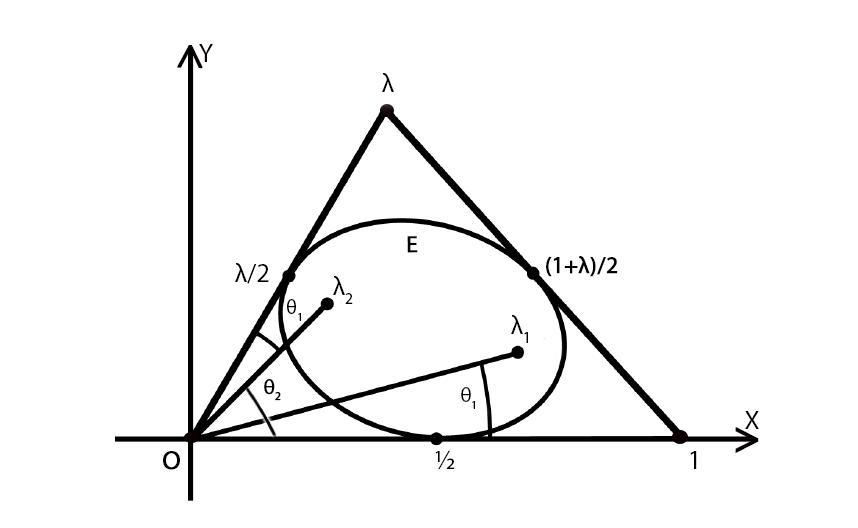Going about the third line segment of the triangle similarly, we can prove the required results easily. I would urge you to try your hand in it. This would then complete the proof of Marden’s result, and maybe you get a chance to present this to “Small Brother” in another dystopian land, and win a reward yourself some time in the future!
This ellipse designed by Marden is a beautiful illustration of geometry and algebra giving birth to something special, known as the Steiner ellipse. I hope this problem would make you think about how a simple algebraic object like a polynomial could give rise to such a lovely geometric phenomenon. The Steiner ellipse also has some other properties- it is the largest ellipse that can be inscribed inside a triangle. It is also the only conic section satisfying these unique tangential clauses. These links are far from rare and are indeed a long-standing drive for mathematicians to establish such beautiful connections.
Bibliography
Satwata Hans is a final year BS-MS student at IISER Kolkata. He is pursuing research in the field of Non Commutative Geometry. When bored of mathematics, he is generally immersed in cinema and music.
signup with your email to get the latest articles instantly